保序回归-IsotonicRegression

发表于 更新于 分类于

1. 保序回归的数学定义

定义：给定一个有限的实数集合 $Y=y_1, y_2, \cdots, y_n$ 代表观察到的响应，以及 $X = x_1, x_2, \cdots, x_n$ 代表未知的响应值，训练一个模型最小化下列方程：

其中 $x_1 \le x_2 \cdots \le x_n$, $w_i$ 为权重是正值，其结果称之为保序回归，而且其解是唯一的。

保序回归的结果是分段函数。

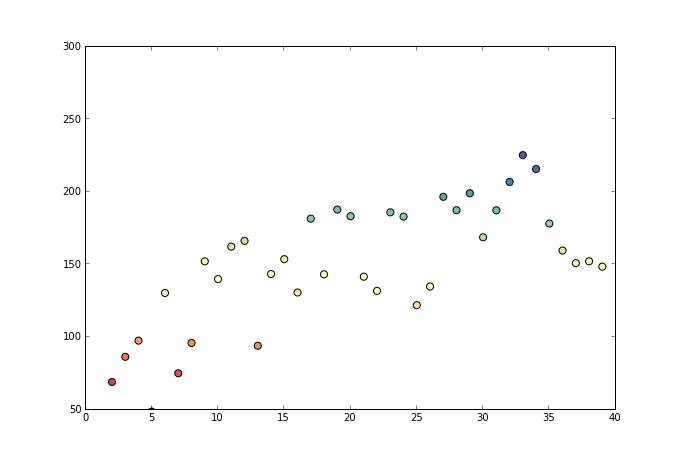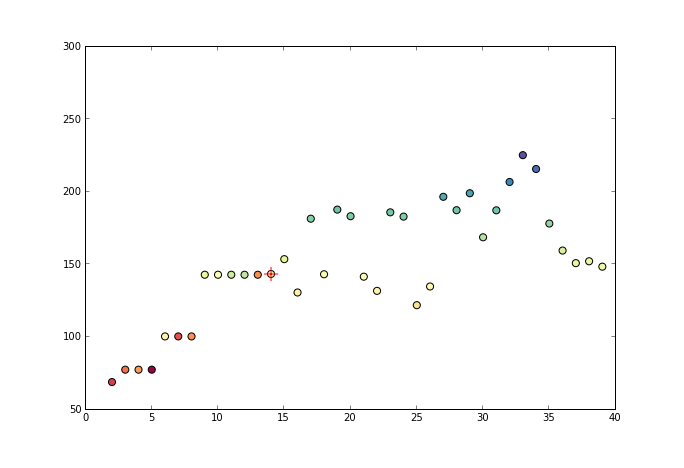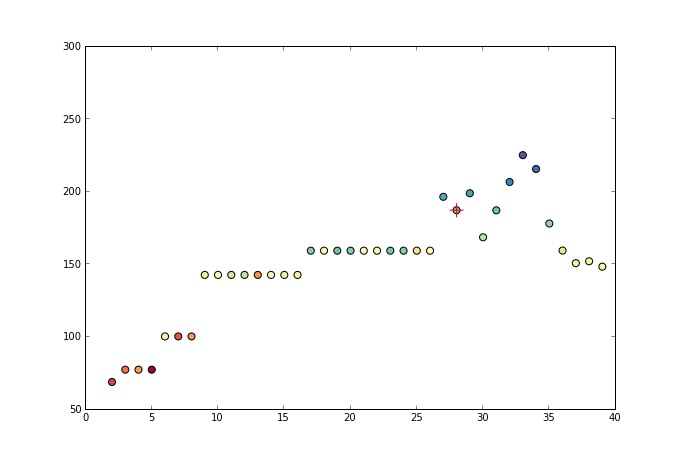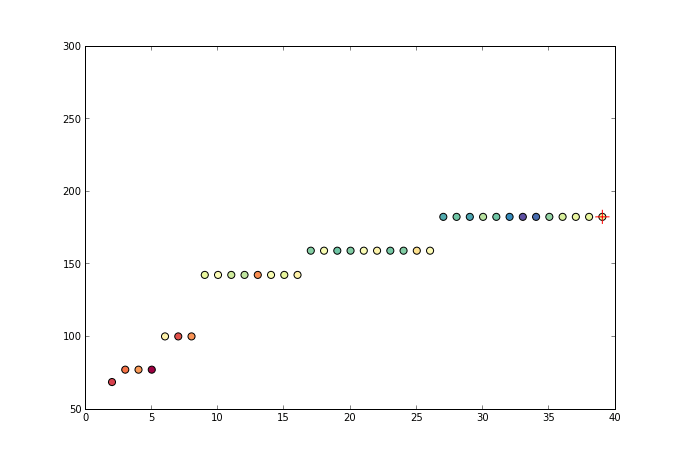
isotonic

2. 举例说明

一般从元素的首元素向后观察，如果出现乱序现象 (当前元素大于后续元素) 时停止观察，并从乱序元素开始逐个向前吸收元素组成一个序列，直达该序列所有元素的平均值小于或是等于下一个待吸收的元素。

  1. 未发现乱序正常读取

    1
    2
    原始序列：<9, 10, 14>
    结果序列：<9, 10, 14>

    分析：从9往后观察，到最后的元素14都未发现乱序情况，不用处理。

  2. 发现乱序，平均值大于后面小于前面

    1
    2
    原始序列：<9, 14, 10>
    结果序列：<9, 12, 12>

    分析：从9往后观察，观察到14时发生乱序 (14 > 10)，停止该轮观察，转入吸收元素处理，从吸收元素10向前一个元素的子序列为 <14, 10>，取该序列所有元素的平均值得12，故用序列 <12, 12> 替代 <14, 10>。吸收10后已经到了最后的元素，处理操作完成。

  3. 发现乱序，平均值大于后面，大于前面

    1
    2
    原始序列：<14, 9, 10, 15>
    结果序列：<11, 11, 11, 15>

    分析：从14往后观察时发生乱序 (14 > 9)，停止该轮观察转入吸收元素处理，吸收元素9后子序列为 <14, 9>。求该序列所有元素的平均值得11.5，由于11.5大于下个待吸收的元素10，所以再吸收10得序列 <14, 10 9,>。求该序列所有元素的平均值得11，由于11小于下个待吸收的元素15，所以停止吸收操作，用序列 <11, 11 11,> 替代 <14, 10 9,>。

3. 官方代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
# Author: Nelle Varoquaux <nelle.varoquaux@gmail.com>
#         Alexandre Gramfort <alexandre.gramfort@inria.fr>
# License: BSD

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.collections import LineCollection

from sklearn.linear_model import LinearRegression
from sklearn.isotonic import IsotonicRegression
from sklearn.utils import check_random_state

n = 100
x = np.arange(n)
rs = check_random_state(0)
y = rs.randint(-50, 50, size=(n,)) + 50. * np.log1p(np.arange(n))

# #############################################################################
# Fit IsotonicRegression and LinearRegression models

ir = IsotonicRegression()

y_ = ir.fit_transform(x, y)

lr = LinearRegression()
lr.fit(x[:, np.newaxis], y)  # x needs to be 2d for LinearRegression

# #############################################################################
# Print data

print("index\tbefore\tafter")
for _x, _y, _y_ in zip(x, y, y_):
	print("{}\t{}\t{}".format(_x, _y, _y_))

# #############################################################################
# Plot result

segments = [[[i, y[i]], [i, y_[i]]] for i in range(n)]
lc = LineCollection(segments, zorder=0)
lc.set_array(np.ones(len(y)))
lc.set_linewidths(np.full(n, 0.5))

fig = plt.figure()
plt.plot(x, y, 'r.', markersize=12)
plt.plot(x, y_, 'b.-', markersize=12)
plt.plot(x, lr.predict(x[:, np.newaxis]), 'b-')
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit', 'Linear Fit'), loc='lower right')
plt.title('Isotonic regression')
plt.show()

输出结果：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
index	before			after
0	-6.0			-6.0
1	31.657359027997266	31.657359027997266
2	68.93061443340548	68.93061443340548
3	86.31471805599453	77.4581957130341
4	97.47189562170502	77.4581957130341
5	48.587973461402754	77.4581957130341
6	130.29550745276566	100.37627113452281
7	74.97207708399179	100.37627113452281
8	95.86122886681098	100.37627113452281
9	152.1292546497023	142.77028731284636
10	139.89476363991855	142.77028731284636
11	162.24533248940003	142.77028731284636
12	166.24746787307683	142.77028731284636
13	93.9528664807629	142.77028731284636
14	143.4025100551105	142.77028731284636
15	153.62943611198907	142.77028731284636
16	130.6606672028108	142.77028731284636
17	181.51858789480823	159.46232588434722
18	143.221948958322	159.46232588434722
19	187.78661367769953	159.46232588434722
20	183.22612188617114	159.46232588434722
21	141.5521226679158	159.46232588434722
22	131.7747107964575	159.46232588434722
23	185.9026915173973	159.46232588434722
24	182.94379124341003	159.46232588434722
25	121.9048269010741	159.46232588434722
26	134.79184330021644	159.46232588434722
27	196.61022550876018	180.64627212456048
28	187.3647914993237	180.64627212456048
29	199.05986908310777	180.64627212456048
30	168.6993602242573	180.64627212456048
31	187.28679513998634	180.64627212456048
32	206.825378073324	180.64627212456048
33	225.31802623080807	180.64627212456048
34	215.76740307447068	180.64627212456048
35	178.1759469228055	180.64627212456048
36	159.54589563221123	180.64627212456048
37	150.87930798631928	180.64627212456048
38	152.1780823064823	180.64627212456048
39	148.4439727056968	180.64627212456048
40	174.6786033352154	180.64627212456048
41	168.88348091416842	180.64627212456048
42	203.0600057846781	180.64627212456048
43	148.20948169591304	180.64627212456048
44	197.33312448851598	181.42419146615785
45	173.43206982445474	181.42419146615785
46	173.50738008550292	181.42419146615785
47	217.56005054539455	183.5004138990913
48	167.59101490553132	183.5004138990913
49	180.6011502714073	183.5004138990913
50	221.59128163621628	183.5004138990913
51	202.56218592907138	183.5004138990913
52	176.5145956776061	183.5004138990913
53	183.44920232821372	183.5004138990913
54	150.36665926162357	183.5004138990913
55	151.26758453675748	183.5004138990913
56	188.1525633917275	183.662501486821
57	206.02215052732095	183.662501486821
58	158.87687219528598	183.662501486821
59	192.71722811110502	183.662501486821
60	172.54369320866556	183.662501486821
61	235.35671925225458	194.14905688424437
62	161.15673631957662	194.14905688424437
63	199.94415416798358	194.14905688424437
64	216.71936349478185	194.14905688424437
65	190.48273710132125	194.14905688424437
66	161.23463096954828	194.14905688424437
67	225.97538525880535	204.21455447880095
68	202.70532522986298	204.21455447880095
69	219.42476210246798	204.21455447880095
70	198.13399385206577	204.21455447880095
71	174.83330595080275	204.21455447880095
72	210.52297205741954	210.52297205741954
73	247.2032546602085	212.9511496110062
74	256.8744056768155	212.9511496110062
75	166.53666701431655	212.9511496110062
76	181.1902710926842	212.9511496110062
77	266.8354413344796	220.28290585628667
78	221.47239262335108	220.28290585628667
79	181.10133173369405	220.28290585628667
80	211.72245773362195	220.28290585628667
81	254.33596236321267	222.26157242700558
82	245.9420303898299	222.26157242700558
83	239.54083994216566	222.26157242700558
84	178.13256282451584	222.26157242700558
85	240.71736481267536	222.26157242700558
86	220.29540593272918	222.26157242700558
87	176.86684072391034	222.26157242700558
88	250.43181848660697	223.73693616781551
89	226.99048351651325	223.73693616781551
90	253.5429753258425	223.73693616781551
91	191.08942885245202	223.73693616781551
92	196.6299746576628	223.73693616781551
93	276.1647391135002	232.61198322512337
94	235.69384458002705	232.61198322512337
95	201.21740957339182	232.61198322512337
96	257.73554892516916	232.61198322512337
97	192.24837393352863	232.61198322512337
98	264.7559925067295	246.50725090306705
99	228.25850929940458	246.50725090306705

pic

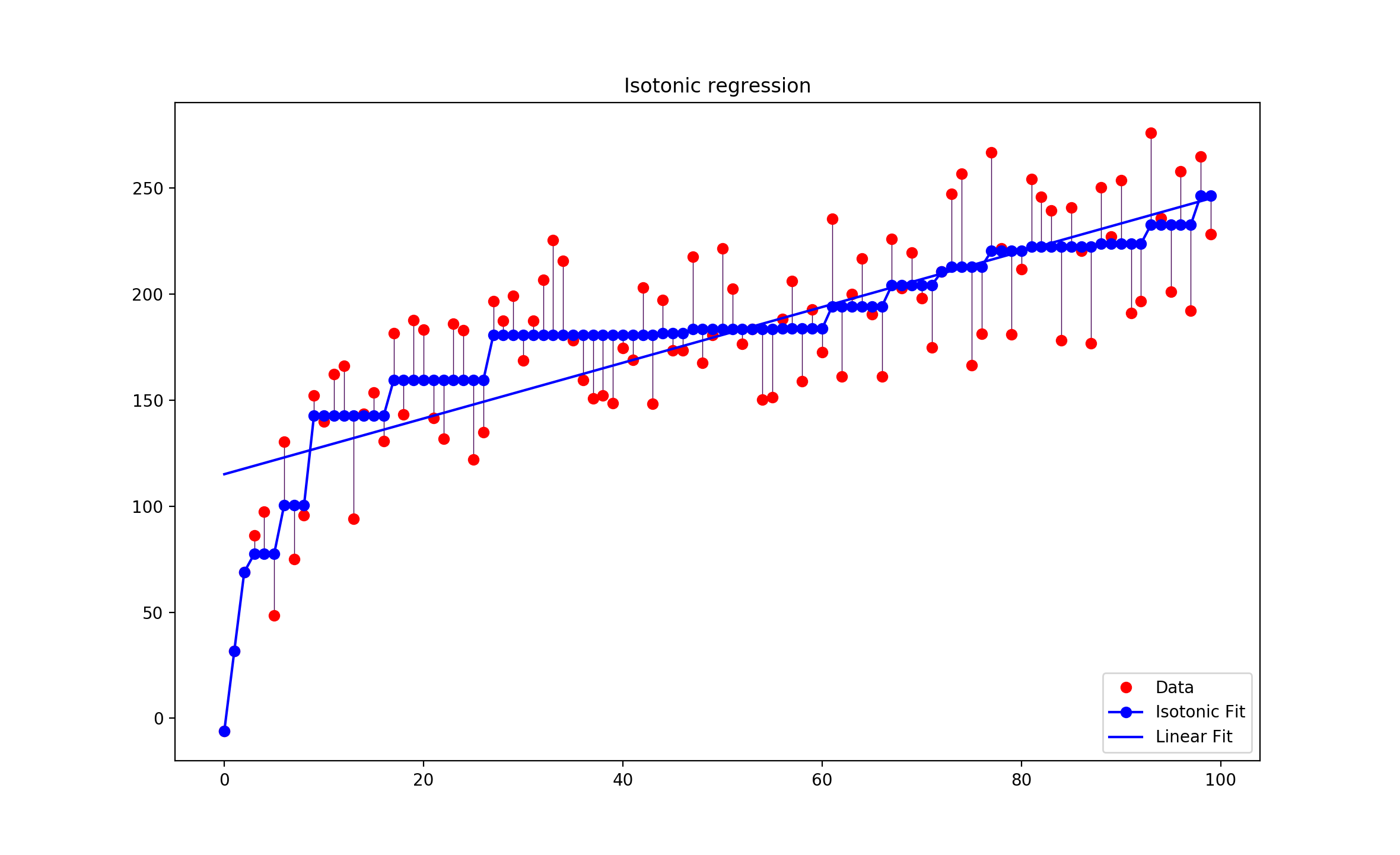
4. 保序回归应用实例

以某种药物的使用量为例，假设药物使用量为数组 $X=0, 1, 2, 3, \cdots, 99$，病人对药物的反应量为$Y = y_1, y_2, y_3, \cdots, y_{99}$ ，而由于个体的原因，$Y$不是一个单调函数(即：存在波动)，如果我们按照药物反应排序，对应的$X$就会成为乱序，失去了研究的意义。而我们的研究的目的是为了观察随着药物使用量的递增，病人的平均反应状况。在这种情况下，使用保序回归，即不改变$X$的排列顺序，又求的$Y$的平均值状况。

从上图中可以看出，最长的蓝线 $x$ 的取值约是$30$到$60$，在这个区间内，$Y$的平均值一样，那么从经济及病人抗药性等因素考虑，使用药量为30个单位是最理想的。

当前IT行业虚拟化比较流行，使用这种方式，找到合适的判断参数，就可以使用此算法使资源得到最大程度的合理利用。

  1. Isotonic Regression-fa.bianp.net
  2. 保序回归 Isotonic Regression-Python
  3. Isotonic regression - wikipedia
  4. Isotonic Regression-sklearn
0%