t-SNE降维

转载自：t-SNE完整笔记

t-SNE(t-distributed stochastic neighbor embedding)是用于降维的一种机器学习算法，是由Laurens van der Maaten 和 Geoffrey Hinton在08年提出来。 此外，t-SNE是一种非线性降维算法，非常适用于高维数据降维到2维或者3维，进行可视化。 t-SNE是由SNE(Stochastic Neighbor Embedding, SNE; Hinton and Roweis, 2002)发展而来。 我们先介绍SNE的基本原理，之后再扩展到t-SNE。最后再看一下t-SNE的实现以及一些优化。

---

1.SNE

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

• SNE构建一个高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有较低的概率被选择。
• SNE在低维空间里在构建这些点的概率分布，使得这两个概率分布之间尽可能的相似。

我们看到t-SNE模型是非监督的降维，它跟k-means等不同，它不能通过训练得到一些东西之后再用于其它数据 (比如k-means可以通过训练得到 k 个点，再用于其它数据集，而 t-SNE 只能单独的对数据做操作，也就是说他只有 fit_transform，而没有fit操作）

SNE是先将欧氏距离转换为条件概率来表达点与点之间的相似度。具体来说，给定 N 个高维的数据 $x_1, …, x_N$ (注意 N 不是维度), t-SNE首先是计算概率$p_{ij}$，正比于$x_i$和$x_j$之间的相似度(这种概率是我们自主构建的)，即：

$$p_{j∣i} = \frac{exp(− ∣∣ x_i − x_j ∣∣ ^2 / (2 \sigma ^2_i))}{ \sum_{k \not= i} exp(− ∣∣ x_i − x_k ∣∣ ^2 / (2 \sigma ^2_i))}$$

这里的有一个参数是$ \sigma_i $，对于不同的点 $x_i$ 取值不一样，后续会讨论如何设置。此外设置 $p_{x∣x} = 0$, 因为我们关注的是两两之间的相似度。

那对于低维度下的$y_i$，我们可以指定高斯分布为方差为$\frac{1}{\sqrt{2}}$，因此它们之间的相似度如下:

$$q_{j∣i} = \frac{ exp(− ∣∣ x_i − x_j ∣∣ ^2)}{ \sum_{k\not=i} exp(−∣∣ x_i − x_k ∣∣ ^2)}$$

同样，设定$q_{i∣i} = 0$。

如果降维的效果比较好，局部特征保留完整，那么 $p_{i∣j} = q_{i∣j}$, 因此我们优化两个分布之间的距离 - KL散度(Kullback-Leibler divergences)，那么目标函数(cost function)如下:

$$C = \sum_{i} KL( P_i ∣∣ Q_i ) = \sum_i \sum_j p_{j∣i} log \frac{p_{j∣i}}{q_{j∣i}}$$

这里的 $P_i$ 表示了给定点 $x_i$ 下，其他所有数据点的条件概率分布。需要注意的是KL散度具有不对称性，在低维映射中不同的距离对应的惩罚权重是不同的， 具体来说：距离较远的两个点来表达距离较近的两个点会产生更大的cost，相反，用较近的两个点来表达较远的两个点产生的cost相对较小 (注意：类似于回归容易受异常值影响，但效果相反)。即用较小的 $q_{j∣i} = 0.2$ 来建模较大的 $p_{j∣i}=0.8$, $cost = p log(\frac{p}{q}) = 1.11$, 同样用较大的 $q_{j∣i}=0.8$ 来建模较大的 $p_{j∣i}=0.2$, $cost = -0.277$, 因此，SNE会倾向于保留数据中的局部特征。

下面我们开始正式的推导SNE。首先不同的点具有不同的 $\sigma_i$，$P_i$ 的熵(entropy)会随着 $\sigma_i$ 的增加而增加。 SNE使用困惑度(perplexity)的概念，用二分搜索的方式来寻找一个最佳的 $\sigma$。其中困惑度指:

$$Perp(P_i) = 2^{H(P_i)}$$

这里的 $H(P_i)$是 $P_i$ 的熵，即:

$$H(P_i) = − \sum_j p_{j∣i} log_2 p_{j∣i}$$

困惑度可以解释为一个点附近的有效近邻点个数。SNE对困惑度的调整比较有鲁棒性，通常选择5-50之间，给定之后，使用二分搜索的方式寻找合适的$\sigma$。

那么核心问题是如何求解梯度了，目标函数等价于 $\sum \sum −p log(q) $这个式子与softmax非常的类似，我们知道softmax的目标函数是 $ \sum −y log p$ ，对应的梯度是$y−p$ (注：这里的softmax中 $y$ 表示label，$p$ 表示预估值)。同样我们可以推导SNE的目标函数中的$i$在$j$下的条件概率情况的梯度是$2 (p_{i∣j} − q_{i∣j})(y_i − y_j) $， 同样$j$在$i$下的条件概率的梯度是 $2 ( p_{j∣i} − q_{j∣i})(y_i − y_j)$，最后得到完整的梯度公式如下:

$$\frac{\partial C}{\partial y_i} = 2 \sum_j (p_{j∣i} − q_{j∣i} + p_{i∣j} − q_{i∣j})(y_i − y_j)$$

在初始化中，可以用较小的 $\sigma$ 下的高斯分布来进行初始化。为了加速优化过程和避免陷入局部最优解，梯度中需要使用一个相对较大的动量(momentum)。 即参数更新中除了当前的梯度，还要引入之前的梯度累加的指数衰减项，如下:

$$Y^{(t)} = Y^{(t−1)} + \eta \frac{\partial C}{ \partial Y} + \alpha (t)( Y^{(t−1)} − Y^{(t−2)})$$

这里的$Y^{(t)}$表示迭代$t$次的解，$\eta$表示学习速率 ，$\alpha (t)$ 表示迭代$t$次的动量。

此外，在初始优化的阶段，每次迭代中可以引入一些高斯噪声，之后像模拟退火一样逐渐减小该噪声，可以用来避免陷入局部最优解。 因此，SNE在选择高斯噪声，以及学习速率，什么时候开始衰减，动量选择等等超参数上，需要跑多次优化才可以。

---

2.t-SNE

尽管SNE提供了很好的可视化方法，但是它很难优化，而且存在”crowding problem”(拥挤问题)。后续中，Hinton等人又提出了t-SNE的方法。与SNE不同，主要如下:

• 使用对称版的SNE，简化梯度公式
• 低维空间下，使用t分布替代高斯分布表达两点之间的相似度

t-SNE在低维空间下使用更重长尾分布的t分布来避免crowding问题和优化问题。在这里，首先介绍一下对称版的SNE，之后介绍crowding问题，之后再介绍t-SNE。

2.1 对称版SNE

优化$p_{i∣j}$和$q_{i∣j}$的KL散度的一种替换思路是，使用联合概率分布来替换条件概率分布，即$P$是高维空间里各个点的联合概率分布，$Q$是低维空间下的，目标函数为:

$$C = KL( P ∣∣ Q) = \sum_i \sum_j p_{i,j} log p_{ij} q_{ij}$$

这里的$p_{ii},q_{ii}$为0，我们将这种SNE称之为symmetric SNE(对称SNE)，因为他假设了对于任意$i, p_{ij} = p_{ji}, q_{ij} = q_{ji} $，因此概率分布可以改写为:

$$p_{ij} = \frac{ exp(−∣∣ x_i − x_j ∣∣ ^2 / 2 \sigma^2)}{\sum_{k\not=l} exp(−∣∣ x_k − x_l ∣∣ ^2 / 2 \sigma^2)} \quad \quad q_{ij} = \frac{exp(−∣∣ y_i − y_j ∣∣^2)}{ \sum_{k≠l} exp(−∣∣ y_k − y_l ∣∣^2)}$$

这种表达方式，使得整体简洁了很多。但是会引入异常值的问题。 比如$x_i$是异常值，那么$∣∣ x_i − x_j ∣∣^2$会很大，对应的所有的$j, p_{ij}$都会很小(之前是仅在$x_i$下很小)，导致低维映射下的$y_i$对cost影响很小。

为了解决这个问题，我们将联合概率分布定义修正为: $p_{ij} = (p_{i∣j} + p_{j∣i}) / 2 $, 这保证了 $\sum_j p_{ij} > \frac{1}{2n}$, 使得每个点对于cost都会有一定的贡献。 对称SNE的最大优点是梯度计算变得简单了，如下:

$$\frac{\partial C}{ \partial y_i} = 4 \sum_j (p_{ij} − q_{ij})(y_i − y_j)$$

实验中，发现对称SNE能够产生和SNE一样好的结果，有时甚至略好一点。

2.2 Crowding问题

拥挤问题就是说各个簇聚集在一起，无法区分。 比如有一种情况，高维度数据在降维到10维下，可以有很好的表达，但是降维到两维后无法得到可信映射， 比如降维如10维中有11个点之间两两等距离的，在二维下就无法得到可信的映射结果(最多3个点)。 进一步的说明，假设一个以数据点$x_i$为中心，半径为$r$的$m$维球(三维空间就是球)，其体积是按$r^m$增长的， 假设数据点是在$m$维球中均匀分布的，我们来看看其他数据点与$x_i$的距离随维度增大而产生的变化。

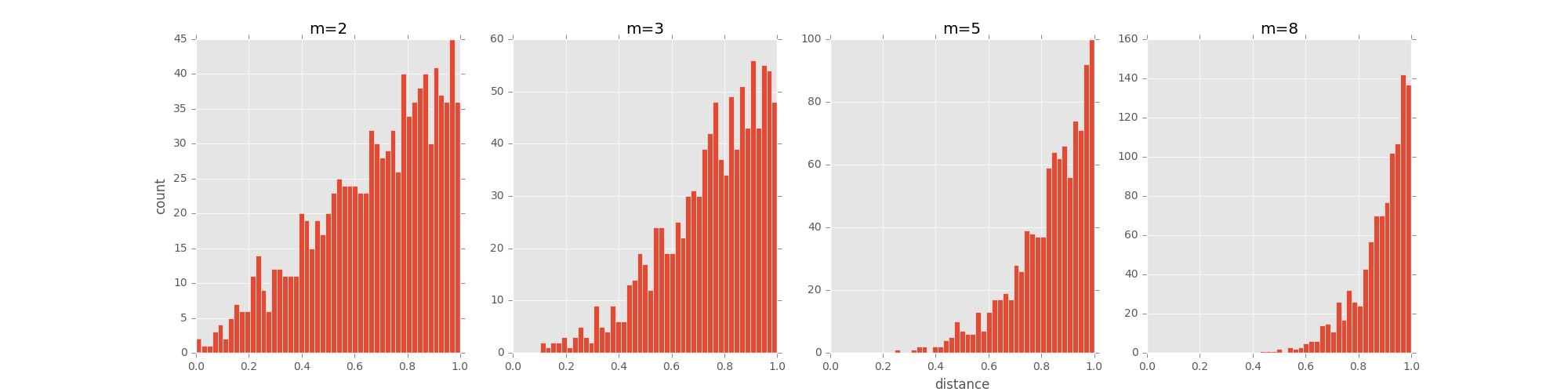
从上图可以看到，随着维度的增大，大部分数据点都聚集在$m$维球的表面附近，与点$x_i$的距离分布极不均衡。如果直接将这种距离关系保留到低维，就会出现拥挤问题。

怎么解决crowding问题呢？

Cook et al.(2007) 提出一种slight repulsion的方式，在基线概率分布(uniform background)中引入一个较小的混合因子 $\rho$， 这样$q_{ij}$就永远不会小于 $ \frac{2 \rho}{n(n-1)}$ (因为一共了n(n-1)个pairs)，这样在高维空间中比较远的两个点之间的$q_{ij}$总是会比$p_{ij}$大一点。 这种称之为UNI-SNE，效果通常比标准的SNE要好。优化UNI-SNE的方法是先让$\rho$为0，使用标准的SNE优化，之后用模拟退火的方法的时候，再慢慢增加$\rho$。 直接优化UNI-SNE是不行的(即一开始$\rho$不为0)，因为距离较远的两个点基本是一样的$q_{ij}$(等于基线分布), 即使$p_{ij}$很大，一些距离变化很难在$q_{ij}$中产生作用。 也就是说优化中刚开始距离较远的两个聚类点，后续就无法再把他们拉近了。

2.3 t-SNE

对称SNE实际上在高维度下另外一种减轻”拥挤问题”的方法：

在高维空间下我们使用高斯分布将距离转换为概率分布，在低维空间下，我们使用更加偏重长尾分布的方式来将距离转换为概率分布，使得高维度下中低等的距离在映射后能够有一个较大的距离。

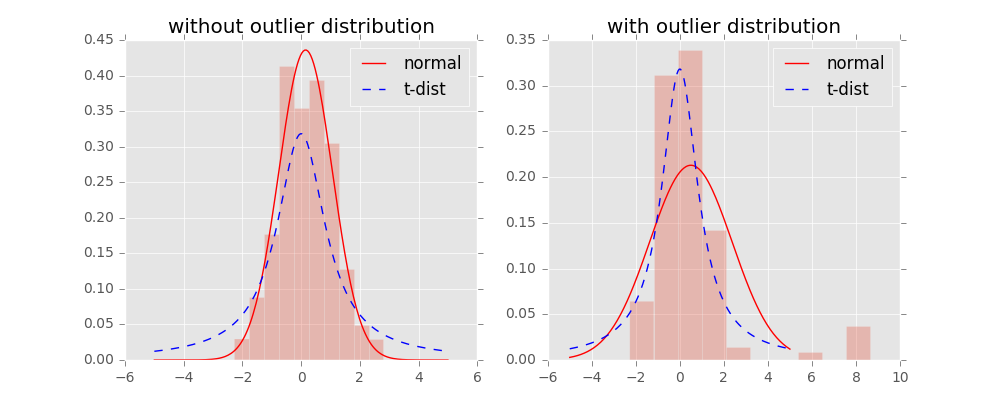
我们对比一下高斯分布和t分布(如上图)，t分布受异常值影响更小，拟合结果更为合理，较好的捕获了数据的整体特征。

使用了t分布之后的q变化，如下:

$$q_{ij} = \frac{(1+∣∣ y_i − y_j ∣∣ ^2)^{−1}}{\sum_{k\not=l} (1 + ∣∣ y_i − y_j ∣∣ ^2)^{−1}}$$

此外，t分布是无限多个高斯分布的叠加，计算上不是指数的，会方便很多。优化的梯度如下:

$$\frac{\partial C}{\partial y_i} = 4 \sum_j ( p_{ij} − q_{ij} ) (y_i − y_j) ( 1 + ∣∣ y_i − y_j ∣∣^2)^{−1}$$

t-SNE的有效性，也可以从上图中看到：

横轴表示距离，纵轴表示相似度, 可以看到，对于较大相似度的点，t分布在低维空间中的距离需要稍小一点； 而对于低相似度的点，t分布在低维空间中的距离需要更远。 这恰好满足了我们的需求，即同一簇内的点(距离较近)聚合的更紧密，不同簇之间的点(距离较远)更加疏远。

总结一下，t-SNE的梯度更新有两大优势：

• 对于不相似的点，用一个较小的距离会产生较大的梯度来让这些点排斥开来。
• 这种排斥又不会无限大(梯度中分母)，避免不相似的点距离太远。

2.4 算法过程

算法详细过程如下：

• Data: $X = x_1, …, x_n$
• 计算cost function的参数：困惑度Perp
• 优化参数: 设置迭代次数T，学习速率$\eta$, 动量$\alpha(t)$
• 目标结果是低维数据表示 $Y^T = y_1, …, y_n$
• 开始优化
  • 计算在给定Perp下的条件概率$p_{j∣i}$ (参见上面公式)
  • 令 $p_{ij} = (p_{j∣i} + p_{i∣j}) / 2n $
  • 用 $N(0, 10^{−4}I)$ 随机初始化 Y
  • 迭代，从 t = 1 到 T， 做如下操作:
    • 计算低维度下的 $q_{ij}$ (参见上面的公式)
    • 计算梯度（参见上面的公式）
    • 更新 $Y^t = Y^{t−1} + \eta \frac{\partial C}{\partial Y} + \alpha (t)(Y^{t−1} − Y^{t−2}) $
  • 结束
• 结束

优化过程中可以尝试的两个trick:

• 提前压缩(early compression):开始初始化的时候，各个点要离得近一点。这样小的距离，方便各个聚类中心的移动。可以通过引入L2正则项(距离的平方和)来实现。
• 提前夸大(early exaggeration)：在开始优化阶段，$p_{ij}$乘以一个大于1的数进行扩大，来避免因为$q_{ij}$太小导致优化太慢的问题。比如前50次迭代，$p_{ij}$乘以4。

2.5 不足

主要不足有四个:

• 主要用于可视化，很难用于其他目的。
  • 比如测试集合降维，因为它没有显式的预估部分，不能在测试集合直接降维；比如降维到10维，因为t分布偏重长尾，1个自由度的t分布很难保存好局部特征，可能需要设置成更高的自由度。
• t-SNE倾向于保存局部特征。
  • 对于本征维数(intrinsic dimensionality)本身就很高的数据集，是不可能完整的映射到2-3维的空间。
• t-SNE没有唯一最优解，且没有预估部分。
  • 如果想要做预估，可以考虑降维之后，再构建一个回归方程之类的模型去做。但是要注意，t-SNE中距离本身是没有意义，都是概率分布问题。
• 训练太慢。有很多基于树的算法在t-SNE上做一些改进

2.6 sklearn中TSNE参数

函数参数表：

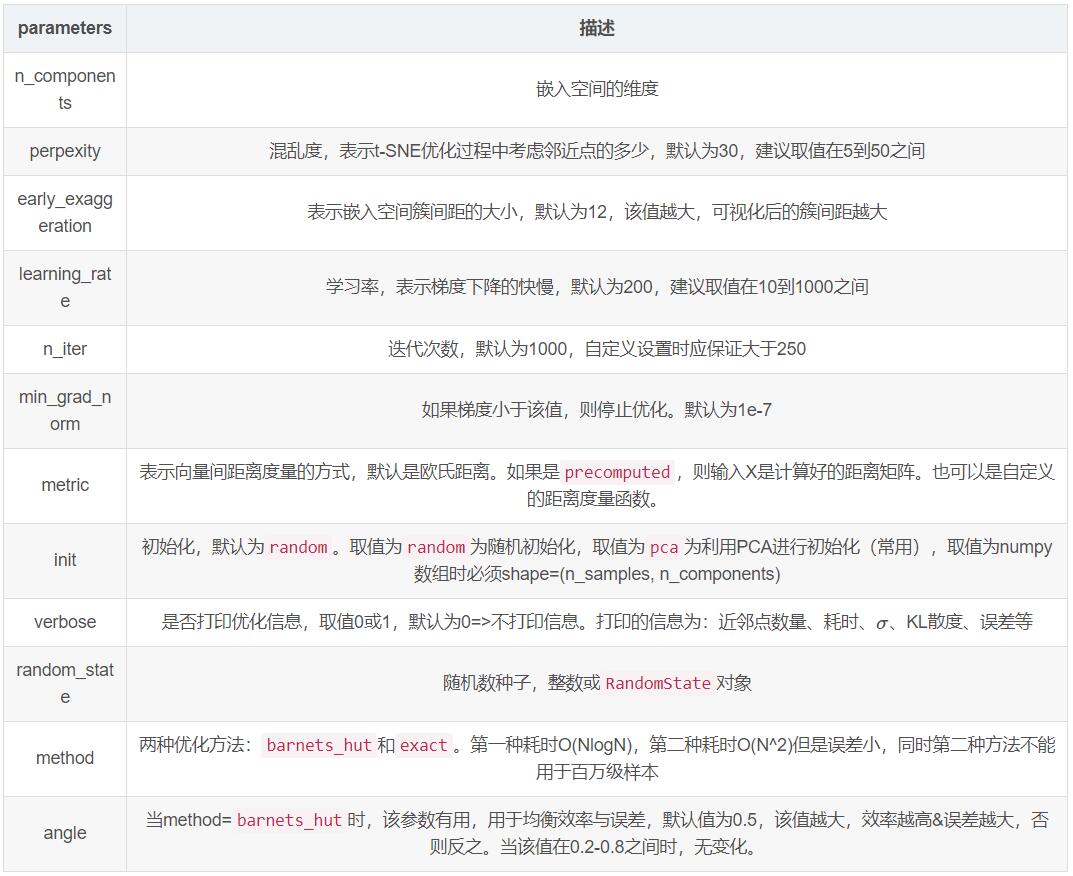
返回对象的属性表：