K-Means聚类

发表于 更新于 分类于

1. 距离量度

1.1 两点之间的距离

  • 欧式距离
  • 曼哈顿距离
  • 切比雪夫距离
  • 余弦距离
  • Jaccard相似系数
  • 相关系数

1.2 两个类别之间的距离

  • 单连接聚类 Single-linkage clustering
    • 一个类的所有成员到另一个类的所有成员之间的最短两个之间的距离
  • 全连接聚类 Complete-linkage clustering
    • 两个类中最远的两个点之间的距离
  • 平均连接聚类 Average-linkage clustering
    • 两个类中的点两两的距离求平均

2. K-Means聚类

算法思想：

  • 选择K个点作为初始质心
  • repeat
    • 将每个点指派到最近的质心，形成K个簇
    • 重新计算每个簇的质心
  • until 簇不发生变化或达到最大迭代次数

这里的重新计算每个簇的质心，如何计算是根据目标函数得来的，因此在开始时需要考虑距离度量和目标函数。


考虑欧几里得距离的数据，使用误差平方和（Sum of the Squared Error, SSE）作为聚类的目标函数，两次运行K均值产生的两个不同的簇集，我们更喜欢SSE最小的那个。

其中$K$表示$K$个聚类中心，$c_i$表示第几个中心，$dist$表示的是欧式距离。

在更新质心时使用所有点的平均值，为什么呢？这里是由SSE决定的。

对第$k$个质心$c_k$求解，最小化式(7)：即对SSE求导并令导数等于零，求解$c_k$，如下：

这样，正如前面所述，簇的最小化SSE的最佳质心是簇中各点的均值。

3. K-Means算法的优缺点

  • 优点
    • 易实现
  • 缺点
    • K值需要预先给定
    • 对初始选取的聚类中心点敏感
    • 可能收敛到局部最小值
    • 在大规模数据收敛慢

进阶学习 bisecting K-means，DBSCAN

4. 算法实现

kmeans.py

4.1 运行结果：

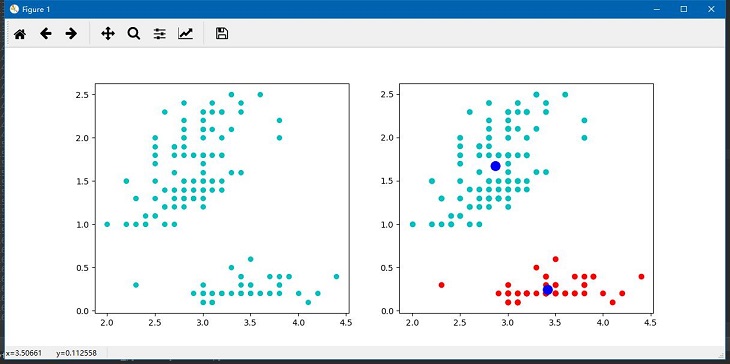
res.jpg

4.2 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
# coding:utf-8

from matplotlib import pyplot as plt
from sklearn import datasets
import numpy as np

def kmeans(data, k=2):
    def _distance(p1, p2):
        tmp = np.sum((p1 - p2) ** 2)
        return np.sqrt(tmp)

    def _rand_center(data, k):
        """Generate k center within the range of data set."""
        n = data.shape[1]  # features
        centroids = np.zeros((k, n))  # init with (0,0)....
        for i in range(n):
            dmin, dmax = np.min(data[:, i]), np.max(data[:, i])
            centroids[:, i] = dmin + (dmax - dmin) * np.random.rand(k)
        return centroids

    def _converged(centroids1, centroids2):
        # if centroids not changed, we say 'converged'
        set1 = set([tuple(c) for c in centroids1])
        set2 = set([tuple(c) for c in centroids2])
        return (set1 == set2)

    n = data.shape[0]  # number of entries
    centroids = _rand_center(data, k)
    label = np.zeros(n, dtype=np.int)  # track the nearest centroid
    assement = np.zeros(n)  # for the assement of our model
    converged = False

    while not converged:
        old_centroids = np.copy(centroids)
        for i in range(n):
            # determine the nearest centroid and track it with label
            min_dist, min_index = np.inf, -1
            for j in range(k):
                dist = _distance(data[i], centroids[j])
                if dist < min_dist:
                    min_dist, min_index = dist, j
                    label[i] = j
            assement[i] = _distance(data[i], centroids[label[i]]) ** 2

        # update centroid
        for m in range(k):
            centroids[m] = np.mean(data[label == m], axis=0)
        converged = _converged(old_centroids, centroids)
    return centroids, label, np.sum(assement)


iris = datasets.load_iris()
X, y = iris.data, iris.target
data = X[:, [1, 3]]  # 为了便于可视化，只取两个维度
# plt.scatter(data[:,0],data[:,1]);

best_assement = np.inf
best_centroids = None
best_label = None

for i in range(10):
    centroids, label, assement = kmeans(data, 2)
    if assement < best_assement:
        best_assement = assement
        best_centroids = centroids
        best_label = label

data0 = data[best_label == 0]
data1 = data[best_label == 1]

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(12, 5))
ax1.scatter(data[:, 0], data[:, 1], c='c', s=30, marker='o')
ax2.scatter(data0[:, 0], data0[:, 1], c='r')
ax2.scatter(data1[:, 0], data1[:, 1], c='c')
ax2.scatter(centroids[:, 0], centroids[:, 1], c='b', s=120, marker='o')
plt.show()
0%