RNN梯度消失、梯度爆炸&LSTM解决梯度消失的办法

发表于 更新于 分类于

目录

  • RNN梯度消失和梯度爆炸的原因
  • LSTM解决梯度消失问题

RNN梯度消失和梯度爆炸的原因

经典的RNN结构如下图所示：

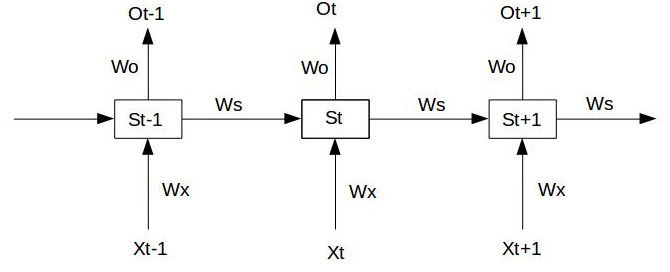
traditional_rnn

假设我们的时间序列只有三段， $S_{0}$ 为给定值，神经元没有激活函数，则RNN最简单的前向传播过程如下：

假设在$t=3$时刻，损失函数为

则对于一次训练任务的损失函数为 $L=\sum_{t=0}^{T}{L_{t}}$ ，即每一时刻损失值的累加。

使用随机梯度下降法训练RNN其实就是对 $W_{x} 、 W_{s} 、 W_{o}$ 以及 $b_{1}、 b_{2}$ 求偏导，并不断调整它们以使$L$尽可能达到最小的过程。

现在假设我们我们的时间序列只有三段，$t1，t2，t3$。

我们只对t3时刻的 $W_{x}、W_{s}、W_{0}$ 求偏导（其他时刻类似）：

可以看出对于 $W_{0}$ 求偏导并没有长期依赖，但是对于 $W_{x}、W_{s}$ 求偏导，会随着时间序列产生长期依赖。因为 $S_{t}$ 随着时间序列向前传播，而 $S_{t}$ 又是 $W_{x}、W_{s}$ 的函数。

根据上述求偏导的过程，我们可以得出任意时刻对 $W_{x}、W_{s}$ 求偏导的公式：

任意时刻对 $W_{s}$ 求偏导的公式同上。

如果加上激活函数， $S_{j}=tanh(W_{x}X_{j}+W_{s}S_{j-1}+b_{1})$ ，

则

激活函数tanh和它的导数图像如下。

tanh

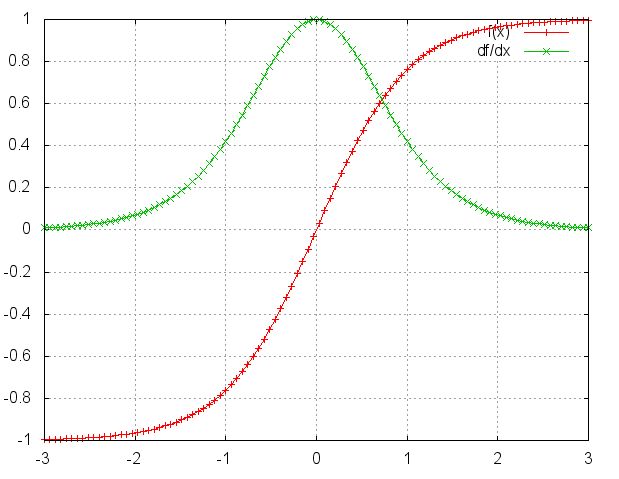
由上图可以看出 $tanh’ \leq 1$ ，对于训练过程大部分情况下$tanh$的导数是小于1的，因为很少情况下会出现 $W_{x}X_{j}+W_{s}S_{j-1}+b_{1}=0$ ，如果 $W_{s}$ 也是一个大于0小于1的值， 则当t很大时 $\prod_{j=k+1}^{t} {tanh’} W_{s}$ ，就会趋近于$0$，和 $0.01^{50}$ 趋近与$0$是一个道理。同理当 $W_{s}$ 很大时 $\prod_{j=k+1}^{t}{tanh^{‘}}W_{s}$ 就会趋近于无穷， 这就是RNN中梯度消失和爆炸的原因。

至于怎么避免这种现象，看看 $\frac{\partial{L_{t}}}{\partial{W_{x}}}=\sum_{k=0}^{t}{\frac{\partial{L_{t}}}{\partial{O_{t}}}\frac{\partial{O_{t}}}{\partial{S_{t}}}}(\prod_{j=k+1}^{t}{\frac{\partial{S_{j}}}{\partial{S_{j-1}}}})\frac{\partial{S_{k}}}{\partial{W_{x}}}$ 梯度消失和爆炸的根本原因就是 $\prod_{j=k+1}^{t}{\frac{\partial{S_{j}}}{\partial{S_{j-1}}}}$ 这一部分，要消除这种情况就需要把这一部分在求偏导的过程中去掉。至于怎么去掉，一种办法就是使 ${\frac{\partial{S_{j}}}{\partial{S_{j-1}}}}\approx1$，另一种办法就是使 ${\frac{\partial{S_{j}}}{\partial{S_{j-1}}}}\approx0$ 。其实这就是LSTM做的事情。

摘自：

RNN梯度消失和爆炸的原因

LSTM解决梯度消失问题

先上一张LSTM的经典图：

LSTM

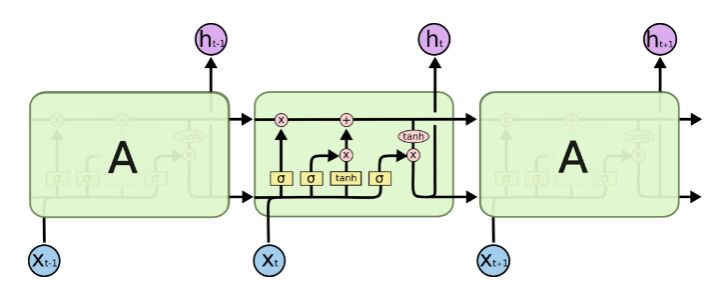
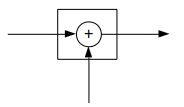
传统RNN可以抽象成下面这幅图：

rnn

而LSTM可以抽象成这样：

LSTM

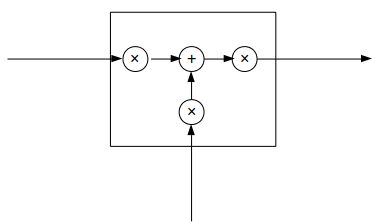
三个 × 分别代表的就是forget gate，input gate，output gate，而我认为LSTM最关键的就是forget gate这个部件。 这三个gate是如何控制流入流出的呢，其实就是通过下面 $f{t},i{t},o_{t}$ 三个函数来控制，因为 $\sigma(x)$（代表sigmoid函数） 的值是介于0到1之间的， 刚好用趋近于0时表示流入不能通过gate，趋近于1时表示流入可以通过gate。

当前的状态 $S_{t}=f_{t}S_{t-1}+i_{t}X_{t}$类似与传统RNN $S_{t}=W_{s}S_{t-1}+W_{x}X_{t}+b_{1}$。将LSTM的状态表达式展开后得：

如果加上激活函数，

RNN梯度消失和爆炸这部分中传统RNN求偏导的过程包含

对于LSTM同样也包含这样的一项，但是在LSTM中

假设 $Z=tanh{‘}(x)\sigma({y})$ ，则 $Z$ 的函数图像如下图所示：

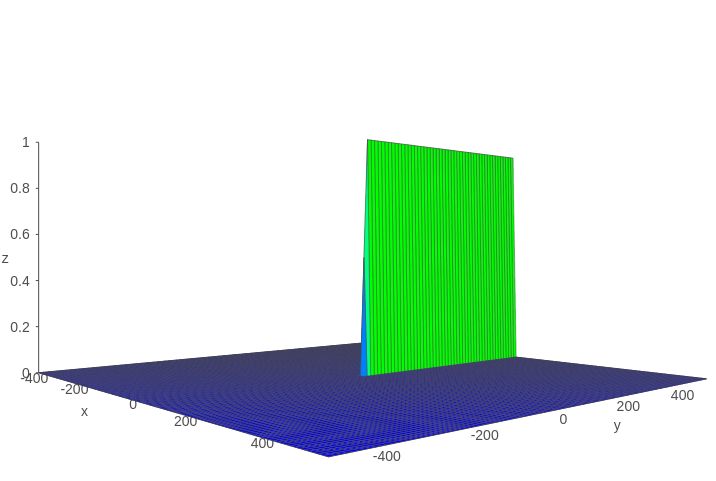
gradient_tanh

可以看到该函数值基本上不是 0 就是 1 。

再看看RNN梯度消失和爆炸原因这部分中传统RNN的求偏导过程：

如果在LSTM中上式可能就会变成：

因为 $\prod_{j=k+1}^{t}\frac{\partial{S_{j}}}{\partial{S_{j-1}}}=\prod_{j=k+1}^{t}{tanh{’}\sigma({W_{f}X_{t}+b_{f}})}\approx 0 | 1 $ ，这样就解决了传统RNN中梯度消失的问题。

摘自：

LSTM如何解决梯度消失问题

0%