LINE Tutorial

目录

• 写作动机
• 引子
• 问题定义
• LINE:大规模信息网络嵌入

---

写作动机

当前大多数图形嵌入方法不能对包含数百万个节点的真实信息网络进行扩展，分析大型信息网络在学术界和行业中一直受到越来越多的关注。 而现在的大多数嵌入方法在小型网络中适用性非常不错，但当网络包含数百万乃至数百亿节点时，就看起来并不那么有效，其时间复杂度至少是节点数的二次方。 最重要的是，它们着重于关注节点之间的一阶相似性，及两点之间是否直接相连，而忽略了其二阶相似性(即拥有许多共同的邻节点)。 因此LINE模型就是为了在信息网络嵌入至低维空间时保留其一阶相似以及二阶相似。

---

引子

下图展示了一个说明性例子。因为顶点6和7之间的边的权值很大，即6和7有非常高的一阶近似，它们应该在嵌入领域中彼此紧密相连。 另一方面，虽然顶点5和6之间的顶点没有链接，但是它们有很多共同的邻域，即它们有很高的二阶近似和两者的表示会是十分的接近。

---

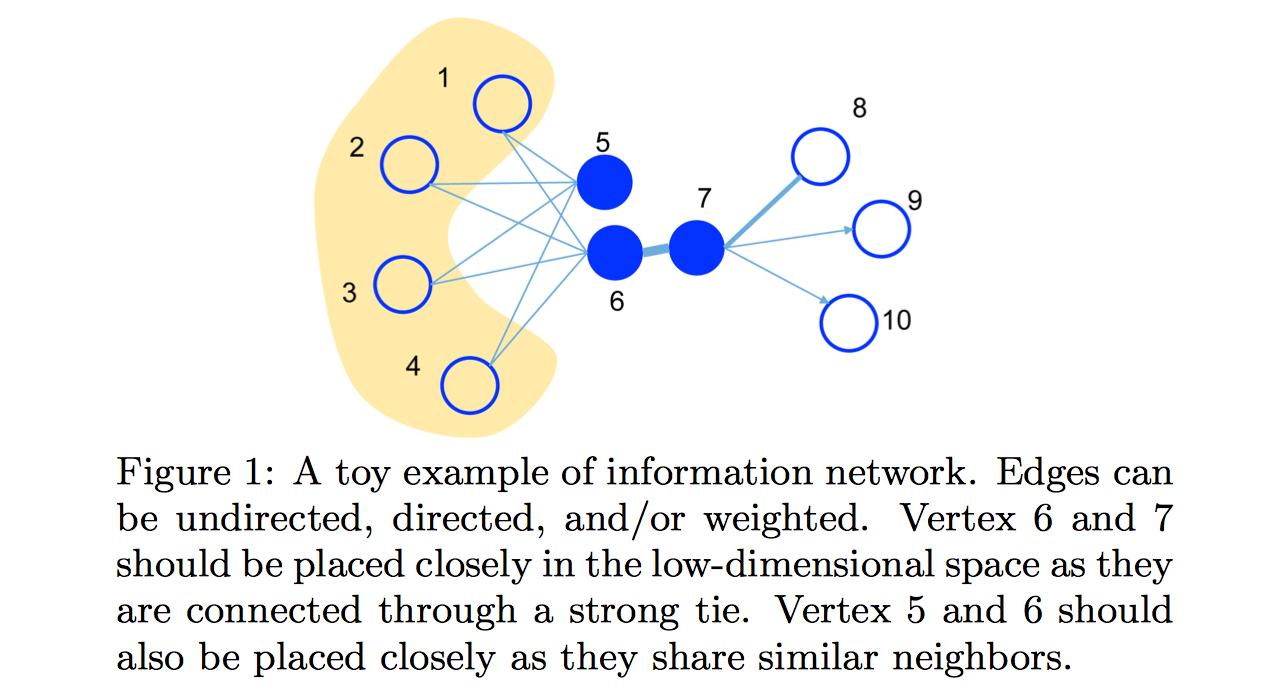
问题定义

• 1.信息网络的定义
  • 信息网络定义为$G=(V,E)$，其中$V$是顶点集合，顶点表示数据对象，$E$是顶点之间的边缘的集合，每条边表示两个数据对象之间的关系。每条边$e\in E$表示为有序对$e=(u,v)$，并且与权重$W{uv} > 0$相关联，权重表示关系的强度。如果$G$是无向的，我们有$(u,v)\equiv (v,u)$和$W{uv}\equiv W{vu}$;如果G是有向的，我们有$(u,v)\ne (v,u)$和$W{uv}\ne W_{vu}$。关于边权重问题，本次论文中只研究非负权重的情况。
• 2.一阶相似性的定义
  • 网络中的一阶相似性是两个顶点之间的局部点对的邻近度。对于由边缘$(u,v)$链接的每对顶点，该边缘的权重$W_{uv}$表示$u$和$v$之间的一阶相似性，如果在$u$和$v$之间没有观察到边缘，它们的一阶相似性为$0$。
• 3.二阶相似度的定义
  • 二阶相似度指的是一对顶点之间的接近程度$(u,v)$在网络中是其邻域网络结构之间的相似性。数学上，让$p{u} =(w{u,1},…,w{u, | V | })$表示一阶附近$u$与所有其他的顶点，那么$u$和$v$之间的二阶相似性由$p{u}$和$p_{v}$之间的相似性来决定。如果没有一个顶点同时和$u$与$v$链接，那么$u$和$v$的二阶相似性是0。
• 4.大规模信息网络嵌入的定义
  • 给定大网络$G=(V,E)$，大规模信息网络嵌入是将每个顶点$v\in V$表示为低维空间$R^{d}$中的向量，学习一个函数$f_{G} : V \rightarrow R^{d}$，其中$d\ll | V |$. 在空间$R^{d}$中，顶点之间的一阶相似性和二阶相似性都被保留。

---

LINE:大规模信息网络嵌入

前文已经提到了信息网络的两大相似性，LINE模型也是由此展开的。

• LINE模型的一阶相似性：对每个无向边$(i,j)$，定义顶点$v_{i}$和$v_{j}$的联合概率分布为：

$$p_1(v_i, v_j) = \frac{1}{1+ exp( - \vec{u}_i^T \cdot \vec{u}_j )}$$

$u_{i}\in {R}^{d}$是顶点$v_{i}$的低维向量表示，为保持其一阶相似性，一种直接方法是最小化以下的目标函数：

$$O_1 = d( \hat{p}_1 (\cdot, \cdot), p_1 (\cdot, \cdot) )$$

$d(\cdot , \cdot)$为两种分布之间的距离，$p(,)$为空间$V\times V$上的一个分布， 其经验分布可以定义为 $ \hat{p}_{1} (i,j) = \frac{ w_{i,j} }{ W } $，其中$ W = \sum_{(i,j) \in E} w_{ij} $。 我们选择尽量减少两个概率分布的KL 散度。将$d(,)$替换为 KL 散度并省略一些常数，我们得到︰

$$O_1 = - \sum_{(i,j) \in E} w_{i,j} log p_1 (v_i, v_j)$$

需要注意的是，一阶相似度仅适用于无向图,而不适用于有向图。

• LINE模型的二阶相似性：二阶相似性假定与其他顶点共享邻居顶点的两个点彼此相似(无向有向均可)，一个向量$u^{} $和$u^{‘}$ 分别表示顶点本身和其他顶点的特定“上下文”，意为二阶相似。对于每个有向边$(i,j)$，我们首先定义由生成“上下文”的概率：

$$p_2(v_j | v_i) = \frac{exp(\vec{u}_j^{'T} \cdot \vec{u}_i)}{\sum_{k=1}^{|V|} exp(\vec{u}_k^{'T} \cdot \vec{u}_i)}$$

可以看到，上式其实是一个条件分布，我们取$i$为研究对象，$p(,v_{i} )$，在降维之后使其接近与经验分布$\hat{p}_{2} $。因此最小化以下目标函数：

$$O_2 = \sum_{i \in V} \lambda_i d ( \hat{p}_2 (\cdot | v_i), p_2(\cdot | v_i) )$$

$d(,)$上文已经说明，$\lambda_{i}$ 来表示网络中顶点$i$的声望,本文中即是顶点$i$的度数，因此二阶相似性的计算公式为：

$$O_2 = - \sum_{(i,j) \in E} w_{i,j} log p_2(v_j | v_i)$$

将上述的$O_{1}$ 以及$O_{2}$ 进行训练，再进行综合。

• 模型优化：$O_{2}$ 的计算代价十分的昂贵，因此优化时使用了负采样方法，为每条边指定了一个目标函数：

$$log \sigma (\vec{u}_j^{'T} \cdot \vec{u}_i) + \sum_{i=1}^K E_{v_n \sim P_n (v)} \left[ log \sigma (- \vec{u}_n^{'T} \cdot \vec{u}_i) \right]$$

其中 $\sigma (x) = 1 / (1+exp(−x))$ 是 sigmoid 函数。这个模型的第一项是观察的边，模型的第二项是从噪声分布中得出的负样例的边 和 K 是负样例的边的数量。 这里设$ P_n (v) \propto d^{3/4}_v $，其中$ d_v $是顶点$ v $的 out-degree。

对于目标函数$O_1$，存在一个非常简单的解：$u_{ik} = \infty$ ，对 $i=1,…, | V | $和 $k=1,…,d$。为了避免这个简单的解，这里仍然可以利用负采样的方法，只需要将$ \vec{v}_j^{‘T} $改为$\vec{v}_j^T$。

这里采样异步随机梯度算法（ASGD）来优化上式。在每一步，ASGD 算法采样一个 mini-batch 的边并更新参数。如果采样了一个边 $(i,j)$，顶点 $i$ 的嵌入向量 $\vec{u}_i$ 梯度会被计算为：

$$\frac{\partial O_2}{\partial \vec{u}_i} = w_{i,j} \cdot \frac{\partial log p_2 (v_j | v_i)}{\partial \vec{u}_i}$$

注意这个梯度是与边的权值相乘，当边的权值有很大的方差的时候会出现问题。例如，在此共现网络中，有些单词共现了很多次但有些词却共现很少次。 在这样的网络中，梯度的比例是发散的，很难找到一个好的学习速率。如果根据小权重的边选择一个大的学习速率，那么在有较大权重的边上的梯度将会爆炸， 如果根据具有较大权重的边来选择学习速率，那么梯度将会变得太小。因此边缘采样同样要优化。从起始边缘采样并将采样的边缘作为二进制边缘，其中采样概率与原始边缘的权重成比例。

---

1. LINE：Large-scale Information Network Embedding
2. LINE:Large-scale Information Network Embedding阅读笔记
3. 论文 LINE：Large-scale Information Network Embedding 阅读笔记