梯度下降
目录
- 1 批量梯度下降BGD
- 2 随机梯度下降SGD
- 3 小批量梯度下降MBGD
在应用机器学习算法时,通常采用梯度下降法来对采用的算法进行训练。其实,常用的梯度下降法还具体包含有三种不同的形式,它们也各自有着不同的优缺点。
下面以线性回归算法来对三种梯度下降法进行比较。
一般线性回归函数的假设函数为: \[ h_{\theta} = \sum_{j=1}^n \theta_j x_j \]
对应的损失函数形式为: \[ J_{train}(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_{\theta} (x^{(i)}) - y^{(i)})^2 \]
其中的\( \frac{1}{2} \)是为了计算方便,上标表示第 i 个样本,下标 j 表示第 j 维度。
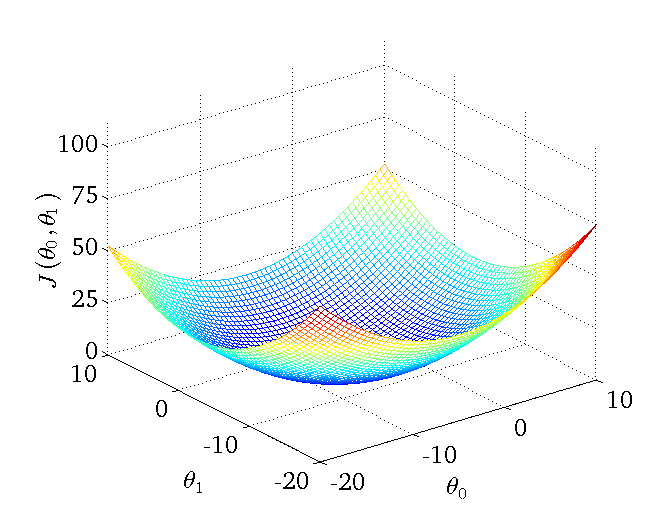
下图为一个二维参数\( \theta_0 \) 和 \( \theta_1 \) 组对应损失函数的可视化图:
1. 批量梯度下降BGD
批量梯度下降法(Batch Gradient Descent,BGD)是梯度下降法最原始的形式,它的具体思路是在更新每一参数时都使用所有的样本来进行更新。 具体的操作流程如下:
- 1 随机初始化\( \theta \);
- 2 更新 \( \theta \)使得损失函数减小,直到满足要求时停止; \[ \theta_j = \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta) \] 这里\( \alpha \)表示学习率。
\[ \begin{equation} \begin{aligned} \frac{\partial}{\partial \theta_j} J(\theta) & = \frac{\partial}{\partial \theta_j} \frac{1}{2} (h_{\theta}(x) - y )^2 \\ & = 2 \cdot \frac{1}{2} ( h_{\theta}(x) - y ) \cdot \frac{\partial}{\partial \theta_j} ( h_{\theta}(x) - y ) \\ & = (h_{\theta}(x) - y ) \cdot \frac{\partial}{\partial \theta_j} \left( \sum_{i=0}^n \theta_i x_i - y \right) \\ & = (h_{\theta}(x) - y) x_j \end{aligned} \end{equation} \]
则对所有数据点,上述损失函数的偏导(累加和)为: \[ \frac{\partial J(\theta)}{\partial \theta_j} = - \frac{1}{m} \sum_{i=1}^m (y^{(i)} - h_{\theta}(x^{(i)})) x_j^{(i)} \]
在最小化损失函数的过程中,需要不断反复的更新\( \theta \)使得误差函数减小,更新方式如下: \[ \theta_j^{‘} = \theta_j + \frac{1}{m} \sum_{i=1}^m ( y^{(i)} - h_{\theta} (x^{(i)}) x_j^{(i)} \]
BGD得到的是一个全局最优解,但是每迭代一步,都要用到训练集所有的数据,如果样本数目 m 很大,那么这种方法的迭代速度很慢! 所以,这就引入了另外一种方法,随机梯度下降。
- 优点:全局最优解;易于并行实现
- 缺点:样本数目很多时,训练过程很慢
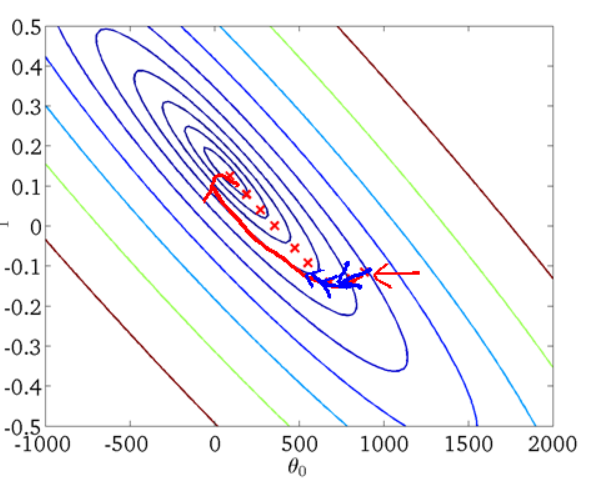
从迭代的次数上来看,BGD迭代的次数相对较少。其迭代的收敛曲线示意图可以表示如下:
2. 随机梯度下降SGD
由于批量梯度下降法在更新每一个参数时,都需要所有的训练样本,所以训练过程会随着样本数量的加大而变得异常的缓慢。 随机梯度下降法(Stochastic Gradient Descent,SGD)正是为了解决批量梯度下降法这一弊端而提出的。
将上面的损失函数写为如下形式: \[ \theta_j^{‘} = \theta_j + ( y^{(i)} - h_{\theta} (x^{(i)}) ) x_j^{(i)} \]
利用每个样本的损失函数对 \( \theta \) 求偏导得到对应的梯度,来更新 \( \theta \):
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将\( \theta\)迭代到最优解了, 对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。 但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。
- 优点:训练速度快
- 缺点:准确度下降,不是全局最优;不易于并行实现
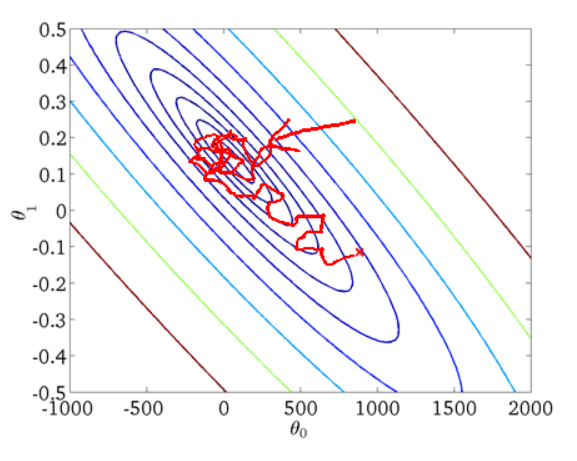
从迭代的次数上来看,SGD迭代的次数较多,在解空间的搜索过程看起来很盲目。其迭代的收敛曲线示意图可以表示如下:
3. 小批量梯度下降MBGD
有上述的两种梯度下降法可以看出,其各自均有优缺点,那么能不能在两种方法的性能之间取得一个折衷呢?即算法的训练过程比较快,而且也要保证最终参数训练的准确率,而这正是小批量梯度下降法(Mini-batch Gradient Descent,MBGD)的初衷。
MBGD在每次更新参数时使用 b 个样本( b一般为10 ),其具体的伪代码形式为:
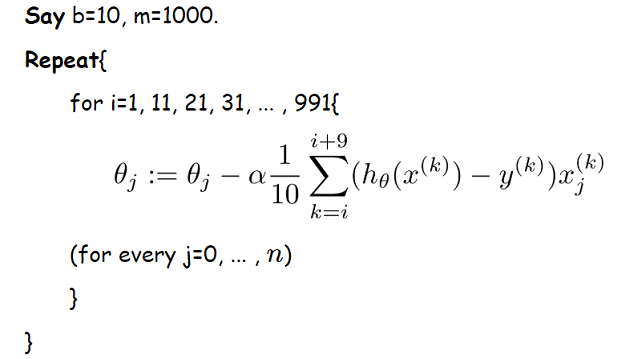
4. 总结
- BGD:每次迭代使用所有的样本;
- SGD:每次迭代使用一个样本;
- MBGD:每次迭代使用 b 个样本;
参考
>