最长回文子串

题目

给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为1000。

示例1：

1
2
3

输入: "babad"
输出: "bab"
注意: "aba"也是一个有效答案。

示例2：

1 2	输入: "cbbd" 输出: "bb"

方法一 - 中心扩展算法

事实上，只需使用恒定的空间，我们就可以在 $ O(n^2) $ 的时间内解决这个问题。

我们观察到回文中心的两侧互为镜像。因此，回文可以从它的中心展开，并且只有 $ 2n - 1 $个这样的中心 [其中自身$ n $个，间隙$ n-1 $个，故可能的中心有$ 2n-1$个]。

int expandAroundCenter(string s, int left, int right)
{
	while (left >= 0 && right < s.length() && s[left] == s[right])
	{  left--; right++; }
	return right - left - 1;
}

string longestPalindrome(string s) 
{ // O(n^2) + O(1)
	int start = 0, length = 0;
	for (int i = 0; i < s.length(); i++)
	{
		int len1 = expandAroundCenter(s, i, i); // i 为中心位置，回文字符奇数个
		int len2 = expandAroundCenter(s, i, i + 1); // i和i+1之间为中心位置，回文字符偶数个
		int len = len1 > len2 ? len1 : len2; // 当前最长的回文串
		if (len > length) // 更新最长的回文串
		{
			start = i - (len - 1) / 2;
			length = len;
		}
	}
	return s.substr(start, length);
}

时间复杂度：$ O(n^2)$，由于围绕中心来扩展回文会耗去 $ O(n)$ 的时间，所以总的复杂度为 $ O(n^2)$。

空间复杂度：$ O(1) $。

方法二 - Manacher算法

首先通过在每个字符的两边都插入一个特殊的符号，将所有可能的奇数或偶数长度的回文子串都转换成了奇数长度。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。

此外，为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

以字符串12212321为例，插入#和这两个特殊符号，变成了T[]=#1#2#2#1#2#3#2#1#，然后用一个数组 P[i] 来记录以字符 T[i] 为中心的最长回文子串向左或向右扩张的长度（包括T[i]，半径长度）。

比如T和P的对应关系：

T # 1 # 2 # 2 # 1 # 2 # 3 # 2 # 1 #
P 1 2 1 2 5 2 1 4 1 2 1 6 1 2 1 2 1

可以看出，P[i]-1正好是原字符串中最长回文串的总长度，为5。

接下来怎么计算 P[i] 呢？Manacher算法增加两个辅助变量C和R，其中C表示最大回文子串中心的位置，R则为C+P[C]，也就是最大回文子串的边界。得到一个很重要的结论：

如果R > i，那么P[i] >= Min(P[2 * C - i], R - i)

下面详细说明这个结论怎么来的

当 R - i > P[j] 的时候，以T[j]为中心的回文子串包含在以T[C]为中心的回文子串中，由于 i 和 j 对称，以T[i]为中心的回文子串必然包含在以T[C]为中心的回文子串中，所以必有 P[i] = P[j]，见下图。

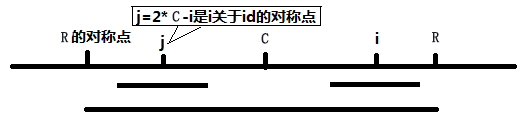
当 R - i <= P[j] 的时候，以T[j]为中心的回文子串不一定完全包含于以T[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以T[i]为中心的回文子串，其向右至少会扩张到R的位置，也就是说 R - i <= P[i]。至于R之后的部分是否对称，就只能老老实实去匹配了。

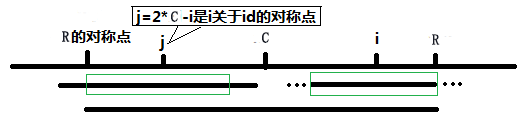
对于 R <= i 的情况，无法对 P[i] 做更多的假设，只能P[i] = 1，然后再去匹配了。

string preProcess(string s) 
{
	int n = s.length();
	if (n == 0) 
		return "^$";
	string ret = "^";
	for (int i = 0; i < n; i++)
		ret += "#" + s.substr(i, 1);
	ret += "#$";
	return ret;
}

string longestPalindrome(string s) 
{
	string T = preProcess(s);
	int n = T.length();
	int* P = new int[n];
	int C = 0, R = 0;
	for (int i = 1; i < n - 1; i++) 
	{
		int j = 2 * C - i; // 等价于 j = C - (i-C) = 2 * C - i

		P[i] = (R > i) ? min(R - i, P[j]) : 0;

		// 尝试拓展中心为i的回文串
		while (T[i + 1 + P[i]] == T[i - 1 - P[i]])
			P[i]++;

		// If palindrome centered at i expand past R, 
		// adjust center based on expanded palindrome.
		if (i + P[i] > R) 
		{
			C = i;
			R = i + P[i];
		}
	}
	// Find the maximum element in P.
	int maxLen = 0;
	int centerIndex = 0;
	for (int i = 1; i < n - 1; i++) 
	{
		if (P[i] > maxLen) 
		{
			maxLen = P[i];
			centerIndex = i;
		}
	}
	delete[] P;
	return s.substr((centerIndex - 1 - maxLen) / 2, maxLen);
}

时间复杂度：$ O(n) $。

空间复杂度：$ O(n) $。

题目

方法一 - 中心扩展算法

方法二 - Manacher算法

参考