Word2Vec Tutorial
目录
- Word2Vec - CBOW
- Word2Vec - Skip-Gram
- Word2Vec的Tricks
自己根据网上资料及自己的理解对word2vec源码阅读并加上注释, 放在我的github weizhaozhao/annotated_word2vec上了, 有兴趣的同学可以一起学习一下,其中的很多tricks都可以尝试应用在实际的工业生产环境中。
1. Word2Vec - CBOW
CBOW是Continuous Bag-of-Words Model的缩写,是一种与前向神经网络语言模型(Neural Network Language Model, NNLM)类似的模型, 不同点在于CBOW去掉了最耗时的非线性隐含层且所有词共享隐含层。
先来模型结构图,如下:
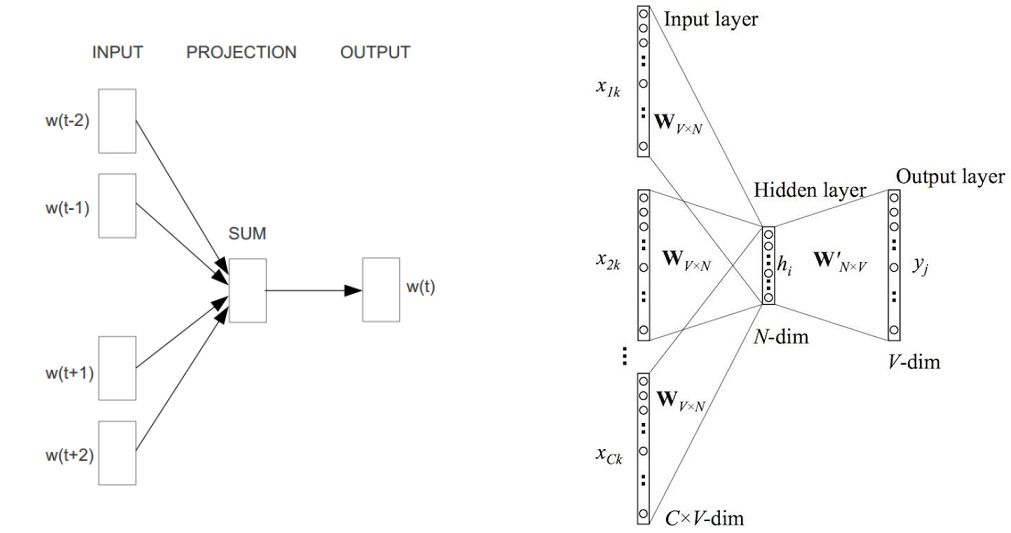
可以看出,CBOW模型是预测\( P(w_t | w_{t-k}, w_{t-(k-1)}, …, w_{t-1}, w_{t+1}, w_{t+2}, …, w_{t+k}) \)。
从输入层到隐含层所进行的实际操作实际就是上下文向量的加和,具体代码如下:
1 | // location: word2vec/trunk/word2vec.c/void *TrainModelThread(void *id) |
其中sentence_position为当前word在句子中的下标,以一个具体的句子A B C D为例,
第一次进入到下面代码时,当前word为A,sentence_position为0,b是一个随机生成的0到window-1的词,
整个窗口的大小为(2 window + 1 - 2 b),相当于左右各看 window-b 个词。可以看出随着窗口的从左往右滑动,
其大小也是随机的 3(b=window-1) 到 2*window+1(b=0) 之间随机变通,即随机值b的大小决定了当前窗口的大小。
代码中的neu1即为隐含层向量,也就是上下文(窗口内除自己之外的词)对应vector之和。
CBOW有两种可选的算法:Hierarchical Softmax 和 Negative Sampling。
Hierarchical Softmax
该算法结合了Huffman编码,每个词w都可以从树的根节点沿着唯一一条路径被访问到。
假设\( n(w,j) \)为这条路径上的第\(j\)个节点,且\( L(w) \)为这条路径的长度,注意\(j\)从1开始编码,即\( n(w,1)=root, n(w,L(w))=w \)。
对于第\(j\)个节点,Hierarchical Softmax算法定义的Lable为 1-code[j],而输出为
\[
f = \sigma ( neu1^T \cdot syn1 )
\]
Loss为负的log似然,即:
\[
Loss = -Likelihood = -(1-code[j]) log f - code[j] log (1-f)
\]
那么梯度为: \[ \begin{equation} \begin{aligned} Gradient_{neu1} & = \frac{\partial Loss}{\partial neu1} \\ & = - (1-code[j]) \cdot (1-f) \cdot syn1 + code[j] \cdot f \cdot syn1 \\ & = - (1-code[j] - f) \cdot syn1 \end{aligned} \end{equation} \]
\[ \begin{equation} \begin{aligned} Gradient_{syn1} & = \frac{\partial Loss}{\partial syn1} \\ & = - (1-code[j]) \cdot (1-f) \cdot neu1 + code[j] \cdot f \cdot neu1 \\ & = - (1-code[j] - f) \cdot neu1 \end{aligned} \end{equation} \]
需要注意的是,word2vec源码中的g实际为负梯度中公共部分与Learningrate alpha的乘积。
1 | // Hierarchical Softmax |
Negative Sampling
在源码中就是随机生成negative个负例(也有可能少于这个数,当随机撞上原来的word跳过)。
原来的word为正例,Label为1,其他随机生成的Lable为0,输出f仍为:
\[
f = \sigma ( neu1^T \cdot syn1 )
\]
Loss为负的Log似然(因采用随机梯度下降法,这里只看一个word中的一层),即:
\[
Loss = -Likelihood = - label \cdot log f - (1-label) \cdot log (1-f)
\]
那么梯度为: \[ \begin{equation} \begin{aligned} Gradient_{neu1} & = \frac{\partial Loss}{\partial neu1} \\ & = -label \cdot (1-f) \cdot syn1 + (1-label) \cdot f \cdot syn1 \\ & = -(label - f) \cdot syn1 \end{aligned} \end{equation} \]
\[ \begin{equation} \begin{aligned} Gradient_{syn1} & = \frac{\partial Loss}{\partial syn1} \\ & = -label \cdot (1-f) \cdot neu1 + (1-label) \cdot f \cdot neu1 \\ & = -(label - f) \cdot neu1 \end{aligned} \end{equation} \]
同样注意代码中g并非梯度,可以看作是乘了Learningrate alpha的error(label与输出f的差)。
1 | // NEGATIVE SAMPLING |
隐含层到输入层的梯度传播
因为隐含层为输入层各变量的加和,因此输入层的梯度即为隐含层的梯度(注意每次循环neu1e都被置零)。
1 | // hidden -> in |
2. Word2Vec - Skip-Gram
Skip-Gram模型的结构与CBOW正好相反,从图中看Skip-Gram应该预测概率\( P(w_i | w_t) \),其中\( t-c \leq i \leq t+c, 且 i \not = t\),
c是决定上下文窗口大小的常数,c越大则需要考虑的pair越多,一般能够带来更精确的结果,但训练时间也会增加。
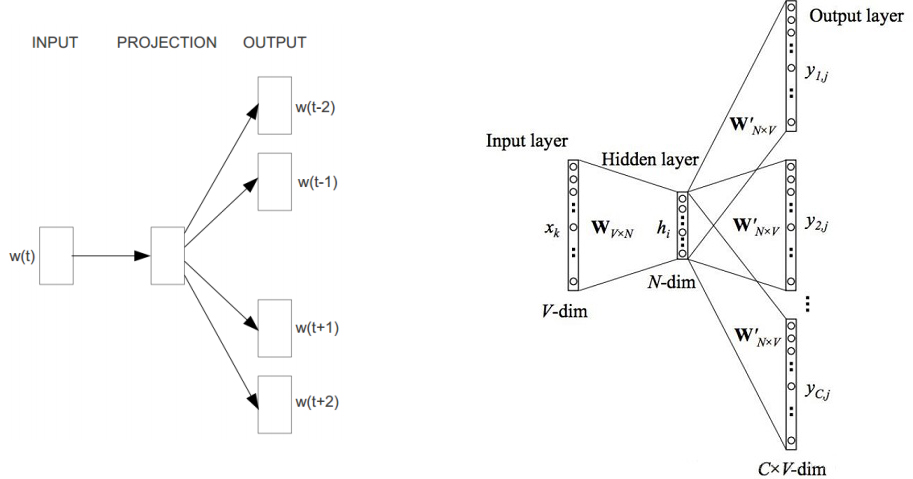
假设存在一个\( w_1, w_2, w_3, …, w_T \)的词组序列,Skip-Gram的目标最大化: \[ \frac{1}{T} \mathop{\sum_{t=1}^T} \mathop{\sum_{-c \leq j \leq c, j \not= 0}} log p(w_{t+j} | w_t) \]
基本的Skip-Gram模型定义\( P(w_o | w_i) \)为: \[ P(w_o | w_i) = e^{v_{w_o}^T v_{w_i}} / \sum_{w=1}^W e^{v_w^T v_{w_i}} \]
从公式中不能看出,Skip-Gram是一个对称的模型,如果\(w_t\)为中心词时,\( w_k \)在其窗口内, 则\( w_t \)也必然在以\( w_k \)为中心词的同样大小的窗口内,也就是: \[ \frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c, j \not=0} log P(w_{t+j} | w_t) = \frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c, j \not=0} log P(w_t | w_{t+j}) \]
同时,Skip-Gram算法中的每个词向量表征了上下文的分布。Skip-Gram中的Skip是指在一定窗口内的词两两会计算概率,即使它们之间隔着一些词, 这样的好处是“白色汽车”和“白色的汽车”很容易被识别为相同的短语。
与CBOW类似,Skip-Gram也有两种可选的算法:Hierarchical Softmax 和 Negative Sampling。
Hierarchical Softmax算法也结合了Huffman编码,每个词w都可以从树的根节点沿着唯一一条路径被访问到。
假设\( n(w,j) \)为这条路径上的第j个节点,且L(w)为这条路径的长度,注意j从1开始编码,即\( n(w,1)=root, n(w, L(w))=w\)。
层级softmax定义的概率\( P(w | w_I) \)为:
\[
P(w | w_I) = \prod_{j=1}^{L(w)-1} \sigma \lbrace \vartheta [ n(w, j+1) = ch(n(w, j)) ] \cdot v_{n(w,j)}^{‘T} v_I \rbrace
\]
其中:
\[
\vartheta(x) =
\begin{cases}
1, \quad if \quad x \quad is \quad true \\
-1, \quad otherwise
\end{cases}
\]
\( ch(n(w, j)) \)既可以是\( n(w,j)\)的左子节点也可以是\( n(w,j) \)的右子节点,word2vec源代码中采用的是左子节点(Label为1-code[j])。
Loss为负的log似然(因为采用随机梯度下降法,这里只看一个pair),即 \[ \begin{equation} \begin{aligned} Loss_pair & = -Log Likelihood_pair \\ & = - log P(w| w_I) \\ & = - \sum_{j=1}^{L(w)-1} log \lbrace \sigma [ \vartheta ( n(w,j+1)=ch(n(w,j)) ) \cdot v_{n(w,j)}^{‘T} v_I ] \rbrace \end{aligned} \end{equation} \]
如果当前节点是左子节点,即\( \vartheta( n(w,j+1)=ch(n(w,j)) ) \)为true
那么\( Loss = - log \lbrace \sigma( v_{n(w,j)}^{‘T} v_I) \rbrace \),则梯度为:
\[ Gradient_{v_{n(w,j)}^{‘}} = \frac{\partial Loss}{\partial v_{n(w,j)}^{‘}} = - (1-\sigma (v_{n(w,j)}^{‘T} v_I)) \cdot v_I \\ Gradient_{v_I} = \frac{\partial Loss}{\partial v_I} = - (1-\sigma (v_{n(w,j)}^{‘T} v_I)) \cdot v_{n(w,j)}^{‘} \]
如果当前节点是右子节点,即\( \vartheta( n(w,j+1)=ch(n(w,j)) ) \)为false
那么\( Loss = - log \lbrace \sigma( - v_{n(w,j)}^{‘T} v_I) \rbrace = - log(1- \sigma(v_{n(w,j)}^{‘T} v_I)) \),则梯度为: \[ Gradient_{v_{n(w,j)}^{‘}} = \frac{\partial Loss}{\partial v_{n(w,j)}^{‘}} = \sigma (v_{n(w,j)}^{‘T} v_I) \cdot v_I \\ Gradient_{v_I} = \frac{\partial Loss}{\partial v_I} = \sigma (v_{n(w,j)}^{‘T} v_I) \cdot v_{n(w,j)}^{‘} \]
合并式(15)和式(16),得:
\[ Gradient_{v_{n(w,j)}^{‘}} = \frac{\partial Loss}{\partial v_{n(w,j)}^{‘}} = - \lbrace 1 - code[j] - \sigma( v_{n(w,j)}^{‘T} v_I) \rbrace \cdot v_I \\ Gradient_{v_I} = \frac{\partial Loss}{\partial v_I} = - \lbrace 1 - code[j] - \sigma( v_{n(w,j)}^{‘T} v_I) \rbrace \cdot v_{n(w,j)}^{‘} \]
此处相关的代码如下,其中g是梯度中的公共部分\( (1-code[j]-\sigma( v_{n(w,j)}^{‘T} v_I)) \)与Learningrate alpha的乘积。
1 | // HIERARCHICAL SOFTMAX |
Negative Sampling和隐层往输入层传播梯度部分与CBOW区别不大,代码如下:
1 | // NEGATIVE SAMPLING |
3. Word2Vec的Tricks
3.1 为什么要用Hierarchical Softmax 或 Negative Sampling?
前面提到到 Skip-Gram 中的条件概率为: \[ P(w_o | w_i) = e^{v_{w_o}^T v_{w_i}} / \sum_{w=1}^W e^{v_w^T v_{w_i}} \]
这其实是一个多分类的 logistic regression, 即 softmax 模型,对应的 label 是 One-hot representation,只有当前词对应的位置为 1,其他为 0。普通的方法是\( p(w_o | w_i) \)的分母要对所有词汇表里的单词求和,这使得计算梯度很耗时。
另外一种方法是只更新当前 \( w_o、 w_i \)两个词的向量而不更新其他词对应的向量,也就是不管归一化项,这种方法也会使得优化收敛的很慢。
Hierarchical Softmax 则是介于两者之间的一种方法,使用的办法其实是借助了分类的概念。假设我们是把所有的词都作为输出,那么“桔子”、“汽车”都是混在一起。而 Hierarchical Softmax 则是把这些词按照类别进行区分的。对于二叉树来说,则是使用二分类近似原来的多分类。例如给定\( w_i \),先让模型判断\( w_o \)是不是名词,再判断是不是食物名,再判断是不是水果,再判断是不是“桔子”。虽然 word2vec 论文里,作者是使用哈夫曼编码构造的一连串两分类。但是在训练过程中,模型会赋予这些抽象的中间结点一个合适的向量, 这个向量代表了它对应的所有子结点。因为真正的单词公用了这些抽象结点的向量,所以Hierarchical Softmax方法和原始问题并不是等价的,但是这种近似并不会显著带来性能上的损失同时又使得模型的求解规模显著上升。
Negative Sampling也是用二分类近似多分类,区别在于使用的是one-versus-one的方式近似,即采样一些负例,调整模型参数使得模型可以区分正例和负例。换一个角度来看,就是 Negative Sampling 有点懒,他不想把分母中的所有词都算一次,就稍微选几个算算,选多少,就是模型中负例的个数,怎么选,一般就需要按照词频对应的概率分布来随机抽样了。
3.2 指数运算
由于 word2vec 大量采用 logistic 公式,所以训练开始之前预先算好这些指数值,采用查表的方式得到一个粗略的指数值。虽然有一定误差,但是能够较大幅度提升性能。代码中的 EXP_TABLE_SIZE 为常数 1000,当然这个值越大,精度越高,同时内存占用也会越多。 MAX_EXP 为常数 6。循环内的代码实质为:
1 | expTable[i] = exp((i -500)/ 500 * 6) 即 e^-6 ~ e^6 |
相当于把横坐标从-6 到 6 等分为 1000 份,每个等分点上(1001个)记录相应的 logistic 函数值方便以后的查询。感觉这里有个bug,第1001个等分点(下标为 EXP_TABLE_SIZE)并未赋值,是对应内存上的一个随机值。
1 | expTable = (real *) malloc((EXP_TABLE_SIZE + 1) * sizeof(real)); |
相关查询的代码如下所示。前面三行保证 f 的取值范围为 [-MAX_EXP,MAX_EXP],这样(f + MAX_EXP)/MAX_EXP/2 的范围为[0,1],那下面的 expTable 的 下标取值范围为[0, EXP_TABLE_SIZE]。一旦取值为 EXP_TABLE_SIZE,就会引发上面所说的 bug。
1 | for (c = 0; c < layer1_size; c++) f += syn0[c + l1] * syn1neg[c + l2]; |
3.3 按word分布随机抽样
word2vec 中的 Negative Sampling 需要随机生成一些负例,通过随机找到一个词和当前 word 组成 pair 生成负例。那么随机找词的时候就要参考每个词的词频,也就是需要根据词的分布进行抽样。 这个问题实际是经典的 Categorical Distribution Sampling 问题。 关于 Categorical Distribution 的基本知识及其抽样可以参考维基百科相关资料:
http://en.wikipedia.org/wiki/Categorical_distribution,
http://en.wikipedia.org/wiki/Categorical_distribution#Sampling
Categorical Distribution Sampling 的基本问题是:已知一些枚举变量(比如index,或者 term 之类)及其对应的概率,如果根据他们的概率分布快速进行抽样。 举例来说:已知字符 a, b, c 出现概率分别为 1/2, 1/3, 1/6,设计一个算法能够随机抽样 a, b, c 使得他们满足前面的出现概率。 维基百科上提到两种抽样方法, 而 word2vec 中的实现采用了一种近似但更高效的离散方法,具体描述如下:
方法一:把类别映射到一条直线上,线段上的点为前面所有类别的概率之和,使用时依次扫描知道改点概率与随机数匹配。
事先准备:
1
2
3
41. 计算每个类别或词的未归一化分布值(对于词来即词频);
2. 把上面计算的值加和,利用这个和进行概率归一化;
3. 引入类别或词的一定顺序,比如词的下标;
4. 计算 CDF(累积分布函数),即把每个点上的值修改为其前面所有类别或词的归一化概率之和。
使用时:
1
2
31. 随机抽取一个 0 到 1 之间的随机数;
2. 定位 CDF 中小于或等于该随机数的最大值,该操作如果使用二分查找可以在 O(log(k))时间内完成;
3. 返回 CDF 对应的类别或词。
使用时的时间复杂度为O(logK),空间复杂度O(K),K为类别数或词数。
方法二:每次抽样n个,如果使用时是一个一个抽的话,可以对这n个进行循环,当然n越大,随机性越好,n与最终的抽样次数尽量匹配比较好。
1 | 1. r = 1; |
这种方法每次可抽n个,随机抽样时的时间复杂度O(1),空间复杂度O(n)。
方法三:即word2vec实现方法
1 | (1) 类似于方法一,先将概率以CDF形式排列在一条线段上,以字符a,b,c出现概率分别为 1/2, 1/3, 1/6 为例,线段如下,左端点为 0,右端点为 1,中间分割点分别为 1/2,(1/2+1/3),(1/2+1/3+1/6) |
该方法不是特别精准,可以无限次抽样,随机抽样时的时间复杂度O(1),空间复杂度O(m),m为离散区间的段数,段数越多越精准,但空间复杂度也越高。
3.4 哈希编码
个比较简单,哈希冲突解决采用的是线性探测的开放定址法。相关代码如下:
1 | // Returns hash value of a word |
3.5 随机数
作者自己编写了随机数生成模块,方法比较简单,就是每次乘以一个很大的数字再加 11 然后取模再归一化。
1 | real ran = (sqrt(vocab[word].cn / (sample * train_words)) + 1) * (sample * train_words) / vocab[word].cn; |
3.6 高频词亚采样
这里的亚采样是指 Sub-Sampling,每个词\( w_i \)被丢弃的概率为: \[ P(w_i) = 1 - \sqrt{\frac{sample}{freq(w_i)}} \]
sample是一个可以设置的参数, demo-word.sh 中是 10-3,\( freq(w_i) \)则为\( w_i \)的词频。具体的实现代码如下:
1 | real ran = (sqrt(vocab[word].cn / (sample * train_words)) + 1) * (sample * train_words) / vocab[word].cn; |
从具体代码可以看出,\(w_i\)被丢弃的概率为: \[ P(w_i) = 1- ( \sqrt{\frac{sample}{freq(w_i)}} + \frac{sample}{freq(w_i)} ) \]
参考
>