EM算法 | Weiguo's Station

最大似然
Jensen不等式
算法推导
算法收敛性
算法举例
代码

最大似然(极大似然)

最大似然估计是一种概率论在统计学的应用，它是参数估计的方法之一。说的是已知某个随机样本满足某种概率分布，但是其中具体的参数不清楚，参数估计就是通过若干次试验，观察其结果，利用结果推出参数的大概值。最大似然估计是建立在这样的思想上:已知某个参数能使这个样本出现的概率最大，当然不会再去选择其他小概率的样本，所以就把这个参数作为估计的真实值。

假设需要调查学校的男生和女生的身高分布。肯定是抽样解决，假设你在校园里随便地询问100个男生和100个女生。他们共200个人(也就是200个身高的样本数据，为了方便表示，下面说“人”的意思即对应其身高)都在教室里面了。那之后怎么办？通过某种办法将男女生分开，然后你就先统计抽样得到的100个男生的身高。假设他们的身高是服从高斯分布的，但是这个分布的均值 $\mu$ 和方差 $\sigma^2$ 不知道，这两个参数是需要估计的。记作 $\theta=[\mu, \sigma]^T$ 。

用数学的语言来说：在学校那么多男生（身高）中，我们独立地按照概率密度 $p(x|\theta)$ 抽取100个（身高）组成样本集 $X$ . 我们想通过样本集 $X$ 来估计出未知参数 $\theta$ 。已知概率密度 $p(x|\theta)$ 是高斯分布 $N(\mu, \sigma)$ 的形式，其中的未知参数是 $\theta=[\mu, \sigma]^T$ 。抽到的样本集是 $X = \lbrace x_1, x_2, … , x_N \rbrace$ ，其中 $x_i$ 表示抽到的第 $i$ 个人的身高，这里 $N$ 就是100，表示抽到的样本个数。

由于每个样本都是独立地从 $p(x| \theta)$ 中抽取的，且可以认为这些男生之间是没有关系的。那么从学校那么多男生中为什么就恰好抽到了这100个人呢？抽到这100个人的概率是多少呢？因为这些男生（的身高）是服从同一个高斯分布 $p(x|\theta)$ 的。那么抽到男生A（的身高）的概率是 $p(x_A | \theta)$ ，抽到男生B的概率是 $p(x_B | \theta)$ 。又因为它们是独立的，所以同时抽到男生A和男生B的概率是 $p(x_A | \theta) \cdot p(x_B | \theta)$ ；同理，我同时抽到这100个男生的概率就是他们各自概率的乘积了。换句话就是从分布是 $p(x | \theta)$ 的总体样本中抽取到这100个样本的概率，也就是样本集X中各个样本的联合概率，用下式表示：

$L(\theta) = L(x_1,…,x_N; \theta) = \mathop{\prod_{i=1}^N} p(x_i;\theta), \quad \theta \in \Theta$

这个概率反映了，在概率密度函数的参数是 $\theta$ 时，得到 $X$ 这组样本的概率。因为这里 $X$ 是已知的，也就是说抽取到的这100个人的身高可以测出来，也就是已知的了。而 $\theta$ 是未知的，则上面这个公式只有 $\theta$ 是未知数，所以它是 $\theta$ 的函数。这个函数放映的是在不同的参数 $\theta$ 取值下，取得当前这个样本集的可能性，因此称为参数 $\theta$ 相对于样本集 $X$ 的似然函数（likehood function）。记为 $L(\theta)$ 。

在学校那么男生中，抽到这100个男生（表示身高）而不是其他人，则表示在整个学校中，这100个人（的身高）出现的概率最大。那么这个概率就可以用上面那个似然函数 $L(\theta)$ 来表示。只需要找到一个参数 $\theta$ ，其对应的似然函数 $L(\theta)$ 最大，也就是说抽到这100个男生（的身高）概率最大。这个叫做 $\theta$ 的最大似然估计量，记为：

$\hat{\theta} = \mathop{\arg\max}_{\theta} L(\theta)$

因此，当知道每个样例属于的分布时，求解分布的参数直接利用最大似然估计或贝叶斯估计法即可。但是对于含有隐变量时，就不能直接使用这些估计方法。EM算法就是含有隐变量的概率模型参数的极大似然估计法。

Jensen不等式

设 $f$ 是定义域为实数的函数，如果对于所有的实数 $x$ ， $f^{\prime \prime}(x) \geq 0$ ，那么 $f$ 是凸函数；当 $x$ 是向量时，如果其hessian矩阵H是半正定的( $H \geq 0$ )，那么 $f$ 是凸函数。如果 $f^{\prime \prime}(x) > 0$ 或者 $H > 0$ ，那么称 $f$ 是严格凸函数。

Jensen不等式表述如下：

如果 $f$ 是凸函数， $X$ 是随机变量，那么 $E[f(X)] \geq f(EX)$ 。特别地，如果 $f$ 是严格凸函数，那么 $E[f(X)]=f(EX)$ 当且仅当 $p(X=EX)=1$ ，也就是说 $X$ 是常量。

下图表示会更清晰：

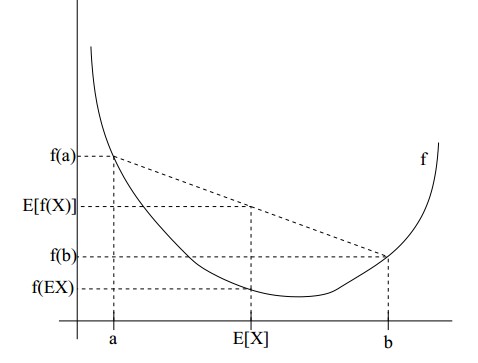
jensen

图中，实线 $f$ 是凸函数， $X$ 是随机变量，有0.5的概率是a，有0.5的概率是b。 $X$ 的期望值就是a和b的中值了。图中可以看到 $E[f(x)] \geq f(EX)$ 成立。

当f是（严格）凹函数当且仅当-f是（严格）凸函数。Jensen不等式应用于凹函数时，不等号方向反向，即 $E[f(X)] \leq f(EX)$ 。

算法推导

给定的训练样本是 $\lbrace x^{(1)},…,x^{(m)} \rbrace$ ，样例间独立，想找到每个样例隐含的类别 $z$ ，能使得 $p(x,z)$ 最大。 $p(x,z)$ 的最大似然估计如下：

$L(\theta) = \mathop{\sum_{i=1}^m} log p(x^{(i)};\theta) = \mathop{\sum_{i=1}^m} log \sum_z p(x^{(i)},z;\theta)$

前一步是对极大似然取对数，后一步是对每个样例的每个可能类别 $z$ 求联合分布概率和。

对于每一个样例 $x^{(i)}$ ，让 $Q_i$ 表示该样例隐含变量 $z$ 的某种分布， $Q_i$ 满足的条件是 $\sum_z Q_i(z) = 1, Q_i(z) \geq 0$ 。（如果 $z$ 是连续性的，那么 $Q_i$ 是概率密度函数，需要将求和符号换做积分符号）。比如要将班上学生聚类，假设隐藏变量 $z$ 是身高，那么就是连续的高斯分布。如果按照隐藏变量是男女，那么就是伯努利分布了。

可以由前面阐述的内容得到下面的公式：

$\begin{equation} \begin{aligned} \sum_i log p(x^{(i)}; \theta) & = \sum_i log \sum_{z} p(x^{(i)}, z; \theta) \\ & = \sum_i log \sum_{z} Q_i(z) \frac{p(x^{(i)}, z; \theta)}{Q_i(z)} \\ & \geq \sum_i \sum_{z} Q_i(z) log \frac{p(x^{(i)}, z; \theta)}{Q_i(z)} \end{aligned} \end{equation}$

第二个等号比较直接，就是分子分母同乘以一个相等的函数；最后不等号利用了Jensen不等式，考虑到 log(x) 是凹函数(二阶导数小于0)。而且 $\sum_{z} Q_i(z) \frac{p(x^{(i)}, z; \theta)}{Q_i(z)}$ 就是 $\frac{p(x^{(i)}, z; \theta)}{Q_i(z)}$ 的期望

这个过程可以看作是对 $L(\theta)$ 求了下界。对于 $Q_i$ 的选择，有多种可能，哪种更好的？假设 $\theta$ 已经给定，那么 $L(\theta)$ 的值就决定于 $Q_i(z)$ 和 $p(x^{(i)}, z)$ 了。可以通过调整这两个概率使下界不断上升，以逼近 $L(\theta)$ 的真实值，什么时候算是调整好了呢？当不等式变成等式时，说明调整后的概率能够等价于 $L(\theta)$ 了。按照这个思路，根据Jensen不等式，等式成立当且仅当随机变量为常数值，即：

$\frac{p(x^{(i)}, z; \theta)}{Q_i(z)} = c$ c为常数，不依赖于 $z$ ；

对此式子做进一步推导，知道 $\sum_z Q_i(z)=1$ ，那么也就有 $\sum_z p(x^{(i)}, z; \theta) = c$ ，那么有下式：

$\begin{equation} \begin{aligned} Q_i(z) & = \frac{p(x^{(i)}, z; \theta)}{\sum_z p(x^{(i)}, z; \theta)} \\ & = \frac{p(x^{(i)}, z; \theta)}{p(x^{(i)}; \theta)} \\ & = p(z | x^{(i)}; \theta) \end{aligned} \end{equation}$

至此，推出了在固定其他参数 $\theta$ 后， $Q_i(z)$ 的计算公式就是后验概率，解决了 $Q_i(z)$ 如何选择的问题。这一步就是E步，建立 $L(\theta)$ 的下界。接下来的M步，就是在给定 $Q_i(z)$ 后，调整 $\theta$ ，极大化 $L(\theta)$ 的下界（在固定 $Q_i(z)$ 后，下界还可以调整的更大）。

那么一般的EM算法的步骤如下：

选择参数的初始值 $\theta^{(0)}$ ，开始迭代；
(E步)对于每一个 $i$ ，计算 $Q_i(z) = p(z | x^{(i)}; \theta^{(t)})$ ；
(M步)计算 $\theta^{(t+1)} = \arg\max_{\theta^{(t)}} \sum_i \sum_{z} Q_i(z) log \frac{p(x^{(i)}, z; \theta^{(t)})}{Q_i(z)}$ ；
重复2-3步，直到收敛。

算法收敛性

假定 $\theta^{(t)}$ 和 $\theta^{(t+1)}$ 是EM第 t 次和 t+1 次迭代后的结果。如果我们证明了 $L(\theta^{(t)}) \leq L(\theta^{(t+1)})$ ，也就是说最大似然估计单调增加，那么最终会到达最大似然估计的最大值。下面来证明，选定 $\theta^{(t)}$ 后，我们得到E步

$Q_i(z) = p(z | x^{(i)}; \theta^{(t)})$

这一步保证了在给定 $\theta^{(t)}$ 时，Jensen不等式中的等式成立，也就是

$L(\theta) = \sum_i \sum_{z} Q_i^{(t)}(z) log \frac{p(x^{(i)}, z; \theta^{(t)})}{Q_i(z)}$

然后进行M步，固定 $Q_i^{(t)}(z)$ ，并将 $\theta^{(t)}$ 视作变量，对上面的 $L(\theta^{(t)})$ 求导后，得到 $L(\theta^{(t+1)})$ ，这样经过一些推导会有以下式子成立：

$\begin{equation} \begin{aligned} L(\theta^{(t+1)}) & \geq \sum_i \sum_{z} Q_i^{(t)}(z) log \frac{p(x^{(i)}, z; \theta^{(t+1)})}{Q_i(z)} \\ & \geq \sum_i \sum_{z} Q_i^{(t)}(z) log \frac{p(x^{(i)}, z; \theta^{(t)})}{Q_i(z)} \\ & = L(\theta^{(t)}) \end{aligned} \end{equation}$

第一个不等号，得到 $\theta^{(t+1)}$ 时，只是最大化 $L(\theta^{(t)})$ ，也就是 $L(\theta^{(t+1)})$ 的下界，而没有使等式成立， 等式成立只有是在固定 $\theta$ ，并按E步得到 $Q_i$ 时才能成立。

况且根据前面得到的下式，对于所有的 $\theta$ 和 $Q_i$ 都成立

$L(\theta) \geq \sum_i \sum_{z} Q_i(z) log \frac{p(x^{(i)}, z; \theta)}{Q_i(z)}$

第二个不等号利用了M步的定义，M步就是将 $\theta^{(t)}$ 调整到 $\theta^{(t+1)}$ ，使得下界最大化。

这样就证明了 $L(\theta)$ 会单调增加。一种收敛方法是 $L(\theta)$ 不再变化，还有一种就是变化幅度很小。

算法举例

假设有两枚硬币A、B，以相同的概率随机选择一个硬币，进行如下的掷硬币实验：共做5次实验，每次实验独立的掷十次，结果如图中a所示，例如某次实验产生了H、T、T、T、H、H、T、H、T、H；(H代表证明朝上)。 a是在知道每次选择的是A还是B的情况下进行，b是在不知道选择的硬币情况下进行，问如何估计两个硬币正面出现的概率？

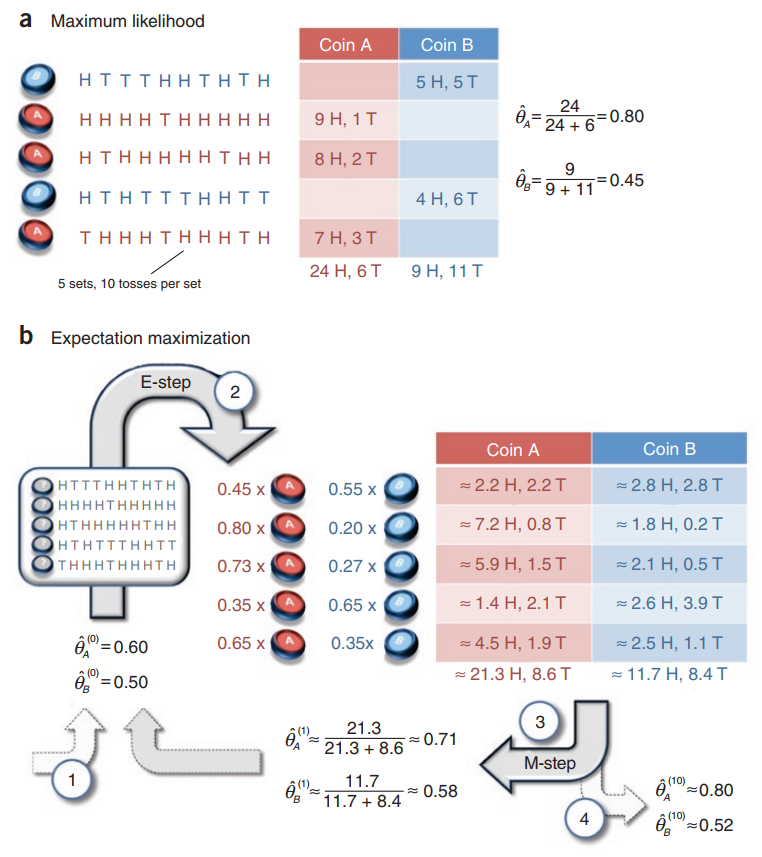
example

针对a情况，已知选择的A or B，重点是如何计算输出的概率分布，论文中直接统计了5次实验中A正面向上的次数再除以总次数作为A的 $\hat{\theta}_A$ ，这其实也是最大似然求导求出来的。

$\begin{equation} \begin{aligned} \mathop{\arg\max}_{\theta} log P(Y | \theta) & = log((\theta_B^5(1-\theta_B)^5) (\theta_A^9(1-\theta_A))(\theta_A^8(1-\theta_A)^2) (\theta_B^4(1-\theta_B)^6) (\theta_A^7(1-\theta_A)^3) ) \\ & = log((\theta_A^{24}(1-\theta_A)^6) (\theta_B^9(1-\theta_B)^{11})) \end{aligned} \end{equation}$

上面这个式子求导之后就能得出 $\hat{\theta}_A = \frac{24}{24+6} = 0.80 以及 \hat{\theta}_B = \frac{9}{9+11} = 0.45$ 。

针对b情况，由于并不知道选择的是A还是B，因此采用EM算法。

E步:计算在给定的 $\hat{\theta}_A^{(0)}$ 和 $\hat{\theta}_B^{(0)}$ 下，选择的硬币可能是A or B的概率，例如第一个实验中选择A的概率为(由于选择A、B的过程是等概率的，这个系数被我省略掉了)

$P(z=A | y_1, \theta) = \frac{P(z=A, y_1 | \theta)}{P(z=A,y_1 | \theta) + P(z=B, y_1 | \theta)} = \frac{0.6^5 \cdot 0.4^5}{0.6^5 \cdot 0.4^5 + 0.5^{10}} = 0.45$

M步:针对Q函数求导，在本题中Q函数形式如下，这里的 $y_j$ 代表的是每次正面朝上的个数。

$\begin{equation} \begin{aligned} Q(\theta, \theta^{(i)}) & = \sum_{j=1}^N \sum_z P(z| y_j, \theta^{(i)}) log P(y_j, z | \theta) \\ & = \sum_{j=1}^N \mu_j log(\theta_A^{y_j} (1-\theta_A)^{10-y_j}) + (1-\mu_j) log(\theta_B^{y_j} (1-\theta_B)^{10-y_j}) \end{aligned} \end{equation}$

从而针对这个式子来对参数求导，例如对 $\theta_A$ 求导

$\begin{equation} \begin{aligned} \frac{\partial Q}{\partial \theta_A} & = \mu_1 (\frac{y_1}{\theta_A} - \frac{10-y_1}{1-\theta_A}) + … + \mu_5 ( \frac{y_5}{\theta_A} - \frac{10-y_5}{1-\theta_5} ) \\ & = \mu_1 ( \frac{y_1 - 10 \theta_A}{\theta_A (1-\theta_A)} ) + … + \mu_5 ( \frac{y_5 - 10 \theta_A}{\theta_A (1-\theta_A)} ) \\ & = \frac{\sum_{j=1}^5 \mu_j y_j - \sum_{j=1}^5 10 \mu_j \theta_A}{\theta_A (1-\theta_A)} \end{aligned} \end{equation}$

求导等于0之后就可得到图中的第一次迭代之后的参数值 $\hat{\theta}_A^{(1)} = 0.71 和 \hat{\theta}_B^{(1)} = 0.58$ 。

这个例子可以非常直观的看出来，EM算法在求解M步是将每次实验硬币取A或B的情况都考虑进去了。

代码

https://blog.csdn.net/u010866505/article/details/77877345

最大似然(极大似然)

Jensen不等式

算法推导

算法收敛性

算法举例

代码

参考