Support Vector Machines - Part 2

支持向量机 - SVM（Support Vector Machines）Part 2

支持向量机 - SVM（Support Vector Machines）Part 1

• 线性可分支持向量机学习算法 - 最大间隔法
• 线性可分支持向量机的对偶算法

支持向量机 - SVM（Support Vector Machines）Part 2

• 线性支持向量机
• 核函数及非线性支持向量机
• 常用的核函数及其特点

支持向量机 - SVM（Support Vector Machines）Part 3

• 序列最小最优化(SMO)算法

支持向量机 - SVM（Support Vector Machines）Part 4

• 支持向量回归 - SVR

目录

• 线性支持向量机
• 核函数及非线性支持向量机
• 常用的核函数及其特点

---

1. 线性支持向量机

线性可分支持向量机的学习方法对于线性不可分训练数据是不适用的，因为问题中的不等式约束并不能都成立，所以我们要修改函数间隔。在支持向量机 - SVM（Support Vector Machines）Part 1中的线性可分支持向量机的约束条件为$y_i(w\cdot x_i +b) \geq 1$，称为硬间隔最大化；现在我们对每个样本$(x_i, y_i)$引入一个松弛变量$\xi_i \geq 0$,使得函数间隔加上松弛变量大于等于1，此时的约束条件就变为

$$y_i(w\cdot x_i +b) \geq 1 - \xi_i$$

同时，对每个松弛变量也要支付一个代价$\xi_i$，目标函数也由原来的$\frac{1}{2} || w ||^2$变为

$$\frac{1}{2} || w ||^2 + C\sum_{i=1}^n \xi_i$$

相对于硬间隔最大化，此时称为软间隔最大化。

线性不可分的线性支持向量机的学习问题变为凸二次规划问题(原始问题)：

$$\mathop{\min_{w,b,\xi}} \frac{1}{2}||w||^2 + C \sum_{i=1}^n \xi_i$$ $$s.j. \quad y_i(w \cdot x_i + b) \geq 1 - \xi_i, \quad i=1,2,...,n$$ $$\xi_i \geq 0, \quad, i=1,2,...,n$$

下面求原始问题的对偶问题：

原始问题的拉格朗日函数是

$$\begin{equation} \begin{aligned} L(w,b,\xi,\alpha,\mu) & = \frac{1}{2}||w||^2 + C \sum_{i=1}^n \xi_i - \sum_{i=1}^n \alpha_i(y_i(w \cdot x_i + b)-1+\xi_i) - \sum_{i=1}^n \mu_i \xi_i \\ & = \frac{1}{2}||w||^2 + C \sum_{i=1}^n \xi_i - \sum_{i=1}^n \alpha_i y_i (w \cdot x +b) + \sum_{i=1}^n \alpha_i - \sum_{i=1}^n \alpha_i \xi_i - \sum_{i=1}^n \mu_i \xi_i \\ s.t. \quad \alpha_i \geq 0, \quad \mu_i \geq 0 \end{aligned} \end{equation}$$

原始问题为

$$\mathop{\min_{w,b,\xi} \max_{\alpha, \mu}} L(w,b,\xi, \alpha, \mu)$$

对偶问题为

$$\mathop{\max_{\alpha, \mu} \min_{w,b,\xi}} L(w,b,\xi, \alpha, \mu)$$

因此，先求$L(w,b,\xi,\alpha,\mu)$对$w,b,\xi$的极小

$$\nabla _w L(w,b,\xi,\alpha,\mu) = w - \sum_{i=1}^n \alpha_i y_i x_i = 0 \\ \nabla _b L(w,b,\xi,\alpha,\mu) = - \sum_{i=1}^n \alpha_i y_i = 0 \\ \nabla_{\xi_i} L(w,b,\xi,\alpha,\mu) = C - \alpha_i - \mu_i = 0$$

得

$$w = \sum_{i=1}^n \alpha_i y_i x_i$$ $$\sum_{i=1}^n \alpha_i y_i = 0$$ $$C - \alpha_i - \mu_i = 0$$

将$ 式(10) \sim 式(12) $代入$式(6)$，得

$$\mathop{\min_{w,b,\xi}} L(w,b,\xi,\alpha,\mu) = - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j x_i^T x_j + \sum_{i=1}^n \alpha_i$$

再对$\mathop{\min_{w,b,\xi}} L(w,b,\xi,\alpha,\mu)$求$\alpha$的极大，即得对偶问题

$$\mathop{\max_{\alpha}} - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j (x_i^T \cdot x_j) + \sum_{i=1}^n \alpha_i$$ $$s.t. \quad \sum_{i=1}^n \alpha_i y_i = 0 \\ C - \alpha_i - \mu_i = 0 \\ \alpha_i \geq 0 \\ \mu_i \geq 0, \quad i=1,2,...,n$$

调整化简约束条件，得

$$\begin{cases} C - \alpha_i - \mu_i = 0 \\ \alpha_i \geq 0 \\ \mu_i \geq 0 \end{cases} \Longrightarrow \begin{cases} \mu_i = C - \alpha_i \geq 0 \\ \alpha_i \geq 0 \end{cases} \Longrightarrow 0 \leq \alpha_i \leq C$$

因此，原始问题的对偶问题为

$$\mathop{\min_{\alpha}} \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j y_i y_j (x_i^T \cdot x_j) - \sum_{i=1}^n \alpha_i$$ $$s.t. \quad \sum_{i=1}^n \alpha_i y_i = 0$$ $$0 \leq \alpha_i \leq C, \quad i=1,2,...,n$$

至此，我们得到一个和线性可分支持向量机对偶问题类似的问题，所以同样需要使用序列最小最优化(SMO)算法解决，详见Support Vector Machines - Part 3。

假设已经求出了$ \alpha^{\ast}=(\alpha_1 ^{\ast}, \alpha_2 ^{\ast}, …, \alpha_n ^{\ast})^T $是对偶问题的解， 若存在$0 \leq \alpha_i \leq C$, 则利用$\alpha^{\ast}$求$w^{\ast}$。

原始问题是凸二次规划问题，解满足$KKT$条件，即得(下列公式也见《统计学习方法》page.111)

$$\nabla _w L(w^{\ast},b^{\ast},\xi,\alpha,\mu) = w^{\ast} - \sum_{i=1}^n \alpha_i^{\ast} y_i x_i = 0 \\ \nabla _b L(w^{\ast},b^{\ast},\xi,\alpha,\mu) = - \sum_{i=1}^n \alpha_i^{\ast} y_i = 0 \\ \nabla_{\xi_i} L(w^{\ast},b^{\ast},\xi,\alpha,\mu) = C - \alpha_i^{\ast} - \mu_i^{\ast} = 0$$ $$\alpha_i^{\ast} (y_i (w^{\ast} \cdot x_i + b^{\ast}) -1 + \xi_i^{\ast}) = 0$$ $$\mu_i^{\ast} \xi_i^{\ast} = (C - \alpha_i^{\ast}) \xi_i = 0 \\ y_i (w^{\ast}\cdot x_i + b^{\ast}) -1 + \xi_i^{\ast} \geq 0 \\ \xi_i^{\ast} \geq 0 \\ \alpha_i^{\ast} \geq 0 \\ \mu_i^{\ast} \geq 0, \quad i=1,2,...,n$$

设我们找到一个支持向量$\alpha_i^{\ast} > 0$，则由$ 式(21)$可以得到

$$y_i (w^{\ast}\cdot x_i + b^{\ast}) -1 + \xi_i^{\ast} = 0 \Longrightarrow b^{\ast} = y_i - \xi_i^{\ast} y_i - w^{\ast} \cdot x_i$$

想要求$b^{\ast}$就必须先求$\xi_i^{\ast}$，没办法得到$\xi_i^{\ast}$，但是如果$\xi_i^{\ast}=0$的话，那么

$$b^{\ast} = y_i - w^{\ast} \cdot x_i$$

所以为了让$\xi_i^{\ast}=0$，那么由$ 式(22) $可知，$C - \alpha_i^{\ast} \not= 0$，即$ \alpha_i^{\ast} \not= C \Rightarrow \alpha_i^{\ast} <C $。

所以，要求解$ b^{\ast} $，则需要找到一个$ 0 < \alpha_i^{\ast} < C $，那么相应的$b^{\ast} $就可以用$式(24)$进行计算。

综合上面的内容，可以看到线性支持向量机(软间隔)和线性可分支持向量机(硬间隔)几乎是一样的。 相对于硬间隔来说，软间隔更灵活，可以通过调节$C$的值来控制，关心分隔超平面的间隔更大一些还是分类错误少一些，并且也不要求我们的数据是线性可分的，所以软间隔比硬间隔更加具有实际的应用价值。

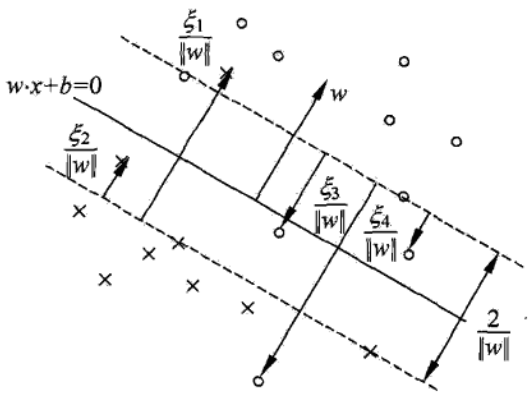
对于$\alpha_i > 0$的样本点$(x_i,y_i)$称为支持向量(软间隔的支持向量)，如下图所示，分离超平面由实线表示，间隔平面用虚线表示。

• $0 < \alpha_i < C, 则\xi_i=0, \quad $分类正确，支持向量落在间隔边界上[类似线性可分支持向量机]
• $\alpha_i = C, 0 < \xi_i < 1, \quad $分类正确，支持向量落在间隔边界和分离超平面之间
• $\alpha_i = C, \xi_i=1, \quad $，支持向量落在分离超平面上
• $\alpha_i = C, \xi_i>1, \quad $，分类错误，支持向量落在超平面另外一侧。

---

2. 核函数及非线性支持向量机

目前为止，SVM还只能处理线性或者近似线性的情况，下面引入核函数，进而将SVM推广到非线性问题上。

对于一个数据点$x$分类，实际上就是通过把$x$带入到$f(x)=wx+b$中算出结果，然后根据结果的正负进行类别的划分，在之前的推导中，我们得到

$$w^{\ast} = \sum_{i=1}^n \alpha_i^{\ast} y_i x_i$$

因此分类函数为

$$\begin{equation} \begin{aligned} f(x) & = (\sum_{i=1}^n \alpha_i^{\ast} y_i x_i)^T x + b \\ & = \sum_{i=1}^n \alpha_i^{\ast} y_i \langle x_i,x \rangle + b \end{aligned} \end{equation}$$

其中$ \langle.,. \rangle $表示内积。这里比较有趣的地方是，对于新点$x$的预测，只需要计算它与训练数据点的内积即可，这是使用核函数$kernel$进行非线性推广的基本前提， 事实上，所有非支持向量的系数$\alpha^{\ast}$都是等于零的，因此对于新点的内积运算，不需要针对所有的训练数据，实际上只要针对少量的支持向量就可以了。

为什么非支持向量的系数为零?

直观解释：间隔边界后面的点对分离超平面的确定没有影响，所以这些无关的点不会参与到分类问题的计算中。

公式解释：在线性可分支持向量机(硬间隔)中，我们得到了拉格朗日函数

$$\begin{equation} \begin{aligned} \theta(w) & = \mathop{\max_{\alpha_i \geq 0}} L(w,b,\alpha) \\ & = \mathop{\max_{\alpha_i \geq 0}} \frac{1}{2}||w||^2 - \sum_{i=1}^n \alpha_i (y_i(wx_i +b)-1) \\ \end{aligned} \end{equation} \alpha_i \geq 0, \quad i=1,2,...,n$$

Notice:

如果$ x_i $是支持向量的话，那么上式右面$ y_i(wx_i +b)-1$部分是等于零的，因为支持向量的函数间隔等于1； 而对于非支持向量，函数间隔大于零，所以$ y_i(wx_i +b)-1$部分是大于零的，所以为了满足拉格朗日最大化，$\alpha_i$必须等于零。

下面开始正式介绍核函数$Kernel$

设$\chi$是输入空间(欧式空间$R^n$的子集或离散集合)，又设$\mathcal{H}$为特征空间(希尔伯特空间[完备的内积空间])，如果存在一个从$\chi$到$\mathcal{H}$的映射

$$\varphi(x): \chi \to \mathcal{H}$$

使得对所有$x,z \in \chi $，函数$K(x,z)$满足条件

$$K(x,z) = \varphi(x) \cdot \varphi(z)$$

则称$K(x,z)$为核函数，$\varphi(x)$为映射函数，式中$\varphi(x) \cdot \varphi(z)$为$\varphi(x)和\varphi(z)$的内积。

核函数的想法是，在学习和预测中只定义核函数$K(x,z)$，而不显式地定义映射函数$\varphi(x)$。通常直接计算$K(x,z)$比较容易，而通过$\varphi(x)和\varphi(z)$计算$K(x,z)$并不容易。

这样，处理非线性数据的情况时，线性支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维空间中学习线性分离超平面，从而把原始空间中不好分的非线性数据分开。 这样分类决策函数变为

$$\begin{equation} \begin{aligned} f(x) & = (\sum_{i=1}^n \alpha_i y_i x_i)^T x + b \\ & = \sum_{i=1}^n \alpha_i y_i K(x_i, x) + b \end{aligned} \end{equation}$$

[其余核函数的举例不再赘述]

维度爆炸的问题！！

按照核函数的定义[先找映射函数，之后再在高维空间中计算内积]，这样是很容易出现维度爆炸问题的。具体例子如下：

设对向量$ x=(u_1, u_2)^T $，映射的结果为

$$\varphi(x)=u_1+u_1^2+u_2+u_2^2+u_1u_2$$

又由于$ x_1=(\eta_1, \eta_2)^T, x_2=(\xi_1, \xi_2)^T $，则$x_1, x_2$的映射如下

$$\varphi(x_1) = (\eta_1, \eta_1^2, \eta_2, \eta_2^2, \eta_1\eta_2) \\ \varphi(x_2) = (\xi_1, \xi_2^2, \xi_2, \xi_2^2, \xi_1\xi_2)$$

上面两式做内积运算即可得到

$$\langle \varphi(x_1), \varphi(x_2) \rangle = \eta_1 \xi_1 + \eta_1^2 \xi_2^2 + \eta_2 \xi_2 + \eta_2^2 \xi_2^2 + \eta_1\eta_2 \xi_1\xi_2$$

另外，如果我们计算下式

$$(\langle x_1, x_2 \rangle + 1)^2 = 2 \eta_1 \xi_1 + \eta_1^2 \xi_2^2 + \eta_2 \xi_2 + \eta_2^2 \xi_2^2 + 2 \eta_1\eta_2 \xi_1\xi_2 + 1$$

对比$式(33)和式(34)$，两者有很多相似的地方。实际上，我们只要把映射的某几个维度线性缩放一下，然后再加上一个常数维度，计算出来的结果和经过映射的两向量内积的结果是相等的。

具体来说，如果对于向量$x=(a,b)^T$，设置新映射如下

$$\phi = (\sqrt{2}a, a^2, \sqrt{2}b, b^2, \sqrt{2}ab, 1)^T$$

则$式(34)$即$(\langle x_1, x_2 \rangle + 1)^2 $的结果和内积$ \langle \phi(x_1), \phi(x_2) \rangle $的结果是相等的。现在我们来研究一下二者的区别。

1. $(\langle x_1, x_2 \rangle + 1)^2 $: 直接在原来的低维空间中进行计算，不需要显示的写出映射后的结果
2. $ \langle \phi(x_1), \phi(x_2) \rangle $：先映射到高维空间中，然后再根据内积进行计算

回到刚才提到的维度爆炸，在$ \langle \phi(x_1), \phi(x_2) \rangle $的方法不能计算的情况下，另一种方法$(\langle x_1, x_2 \rangle + 1)^2 $却能从容处理，甚至无穷维度的情况也可以计算。 这也就是核函数不显式的求映射关系，直接在低维计算，高维学习分离超平面的原因之一。

这样，我们之前学习到的线性支持向量机，可以通过核函数学习非线性数据的情况：

$$f(x) = \sum_{i=1}^n \alpha_i y_i \langle x_i, x \rangle + b \Longrightarrow f(x)= \sum_{i=1}^n \alpha_i y_i K(x_i, x) + b$$

---

3. 常用的核函数及其特点：

• 多项式核函数(polynomial kernel function)

  $$K(x_1, x_2) = (\langle x_1, x_2 \rangle + R)^d$$

  该空间的维度是$C_{m+d}^d$,其中$m$是原始空间的维度。

• 高斯核函数(Gaussian kernel function) / 高斯径向基函数(Radial basis function)

  $$K(x_1, x_2) = exp(- \frac{|| x_1 - x_2 ||^2}{2\sigma^2})$$

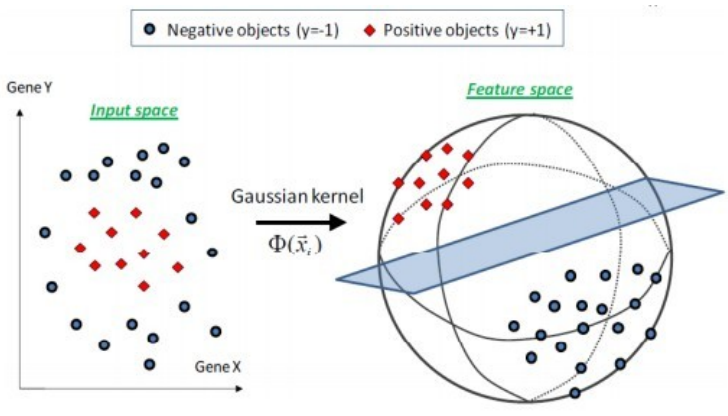
  这个核会将原始空间映射为无穷维空间。不过，如果$\sigma$选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间； 反过来，如果$\sigma$选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。 不过，总的来说，通过调控参数$\sigma$，高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。下图所示的例子便是把低维线性不可分的数据通过高斯核函数映射到了高维空间。

• 线性核函数 $$K(x_1, x_2) = \langle x_1, x_2 \rangle$$ 这实际上就是原始空间中的内积。这个核存在的主要目的是使得“映射后空间中的问题”和“映射前空间中的问题”两者在形式上统一起来了 (意思是说，咱们有的时候，写代码，或写公式的时候，只要写个模板 或通用表达式，然后再代入不同的核，便可以了，于此，便在形式上统一了起来，不用再分别写一个线性的，和一个非线性的)

更多核函数进阶请看这里

last but not least.

核函数的本质

1. 实际中，我们会经常遇到线性不可分的样例，此时，我们的常用做法是把样例特征映射到高维空间中去；
2. 但进一步，如果凡是遇到线性不可分的样例，一律映射到高维空间，那么这个维度大小是会高到可怕的(即维度爆炸)；
3. 核函数登场，核函数的价值在于它虽然也是将特征进行从低维到高维的转换，但核函数事先在低维上进行计算，而将实质上的分类效果表现在了高维上，也就如上文所说的避免了直接在高维空间中的复杂计算。

核函数选择问题

需要注意的是需要对数据归一化处理

1. 如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM
2. 如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel
3. 如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况

---

参考

李航 - 《统计学习方法》

July - 支持向量机通俗导论（理解SVM的三层境界）

学习July博文总结——支持向量机(SVM)的深入理解

周志华 - 《机器学习》

_席达_ - SVM学习笔记