决策树 Decision Tree

决策树 - Decision Tree

目录

• ID3
• C45
• 决策树的剪枝
• CART
• 特点
• 代码实现

---

决策树学习的3个步骤：

• 特征选择
• 决策树生成
• 决策树修剪

决策树的损失函数通常为正则化的极大似然函数。

---

1. ID3

ID3算法使用信息增益作为特征选择的标准，信息增益越大越好。

1.1 信息增益算法

输入：

训练数据集 $ D $ 和特征 $ A $;

输出：

特征$A$对训练数据集$D$的信息增益 $ g(D,A) $

（1）计算数据集 $ D $ 的经验熵 $ H(D) $

$$H(D) = - \sum_{k=1}^K \frac{ | C_k |}{| D |}log_2 \frac{| C_k |}{| D |}$$

（2）计算特征$A$对数据集$D$的经验条件熵$ H(D | A) $

$$H(D | A) = \sum_{i=1}^n \frac{| D_i |}{| D |} H(D_i) = - \sum_{i=1}^n \frac{ | D_i | }{ | D | } \sum_{k=1}^K \frac{| D_{ik} |}{ | D_i |} log_2 \frac{ | D_{ik} |}{| D_i |}$$

（3）计算信息增益

$$g(D,A) = H(D) - H(D | A)$$

其中$K$为类别的数量$ \lbrace C_1, C_2, …, C_k \rbrace $，$n$为特征$A$的取值数量$ \lbrace a_1, a_2, …, a_n \rbrace $。

---

2. C45

信息增益作为标准时，存在偏向于取值数量较多的特征的问题，因此C45算法选择信息增益比作为划分的标准，信息增益比越大越好。

2.1 信息增益比(基于信息增益)

定义为信息增益$g(D,A)$与关于特征$A$的值的熵$H_A(D)$之比，即：

$$g_R(D,A) = \frac{g(D,A)}{H_A(D)}$$ $$H_A(D) = - \sum_{i=1}^n \frac{ | D_i | } { | D | } log_2 \frac{ | D_i | }{ | D |}$$

其中$n$为特征$A$取值的个数。

---

3. 决策树的剪枝

设树$ T $的叶结点个数为$ | T | $，$t$是树$T$的叶结点，该叶结点有$N_t$个样本点，其中$k$类的样本点有$N_{tk}$个，$k=1,2,…,K$，$H_t(T)$为叶结点上的经验熵，则决策树的损失函数可以定义为：

$$\begin{equation} \begin{aligned} C_{\alpha}(T) & = \sum_{t=1}^{ | T | } N_t H_t(T) + \alpha | T | \\ & = - \sum_{t=1}^{ | T | } \sum_{k=1}^K N_{tk} log \frac{N_{tk}}{N_t} + \alpha | T | \\ & = C(T) + \alpha | T | \end{aligned} \end{equation}$$

通过 $ \alpha \geq 0 $控制模型与训练数据拟合度和模型复杂度。

3.1 ID3&C45树的剪枝算法

输入：生成算法产生的整个树 $ T $，参数 $ \alpha $；

输出：修剪后的子树$ T_{\alpha} $。

（1）计算每个结点的经验熵, 经验熵计算公式；

$$H_t(T) = - \sum_k \frac{N_{tk}}{N_t} log \frac{N_{tk}}{N_t}$$

（2）递归地从树的叶结点向上回缩；

设一组叶结点回缩到其父结点之前与之后的整体树分别为$T_B$与$T_A$，其对应的损失函数值分别为$C_{\alpha}(T_B)$与$C_{\alpha}(T_A)$，如果

$$C_{\alpha}(T_B) \leq C_{\alpha}(T_A)$$

则进行剪枝，即将父结点变为新的叶结点。

（3）返回（2），直至不能继续为止，得到损失函数最小的子树$T_{\alpha}$。

---

4. CART

CART假设决策树是二叉树，内部结点特征取值为“是”和“否”，递归二分每个特征。

• 回归数使用平方误差最小化准则，越小越好。
• 分类数使用基尼指数最小化准则，越小越好。

4.1 回归树

输入：训练数据集$ D=\lbrace (x_1, y_1), (x_2, y_2), …, (x_N, y_N) \rbrace $, 并且$Y$是连续型变量；

输出：回归树 $ f(x) $

在训练数据集所在的输入空间中，递归地将每个区域划分为两个子区域并决定每个子区域上的输出值，构建二叉决策树。

（1）选择最优切分变量$j$与切分点$s$，求解

$$\mathop{\min}_{j,s} [\mathop{\min}_{c_1} \sum_{x_i \in R_1(j,s)} (y_i - c_1)^2 + \mathop{\min}_{c_2} \sum_{x_i \in R_2(j,s)} (y_i - c_2)^2]$$

遍历$j$，对固定的切分变量$j$扫描切分点$s$，选择使得上式达到最小值的对$(j,s)$。

（2）用选定的对$(j,s)$划分区域并决定相应的输出值(均值)：

$$R_1(j,s) = \lbrace x | x^{(j)} \leq s \rbrace, \quad R_2(j,s)=\lbrace x | x^{(j)} > s \rbrace \\ \hat{c}_m = \frac{1}{N_m} \sum_{x_i \in R_m(j,s)} y_i, \quad x \in R_m, \quad m=1,2$$

（3）继续对两个子区域调用步骤(1),(2)，直至满足停止条件；

（4）将输入空间划分为$M$个区域$ R_1, R_2, …, R_M $，生成决策树：

$$f(x) = \sum_{m=1}^M \hat{c}_m I(x \in R_m)$$

4.2 分类树

在特征$ A $的条件下，集合$ D $的基尼指数定义为

$$\begin{equation} \begin{aligned} Gini(D, A) & = \frac{ | D_1 | }{ | D | } Gini(D_1) + \frac{ | D_2 | }{ | D | } Gini(D_2) \\ & = \frac{ | D_1 | }{ | D | } [1 - \sum_{k=1}^K(\frac{ | C_k | }{ | D_1 | })^2 ] + \frac{ | D_2 | }{ | D | } [1 - \sum_{k=1}^K(\frac{ | C_k | }{ | D_2 | })^2 ] \end{aligned} \end{equation}$$

其中$ C_k $是$ D_i $中属于第$k$类的样本子集，$K$是类的个数。

输入：训练集$D$,停止计算的条件

输出：CART决策树

根据训练集，从跟结点开始递归地对每个结点进行一下操作，构建二叉决策树。

（1）根据每一个特征以及每个特征的取值，计算相应二叉划分时的基尼指数；

（2）在所有可能的特征及可能的特征值中，选择基尼指数最小的特征及相应特征值作为划分切分特征及切分点，并将训练集划分到两个子结点中；

（3）对两个子节点递归调用(1),(2)，直至满足停止条件；

（4）生成CART决策树。

4.3 CART的剪枝算法

• 1. 剪枝，形成一个子树序列

在剪枝过程中，计算子树的损失函数：

$$C_{\alpha}(T) = C(T) + \alpha | T |$$

其中，$T$为任意子树，$C(T)$表示训练数据的预测误差，$| T |$为子树的叶结点数目，$ \alpha \geq 0 $为参数。

具体地，从整体树$T_0$开始剪枝，对$T_0$的任意内部结点$t$，以$t$为单结点树的损失函数是

$$C_{\alpha}(t) = C(t) + \alpha$$

以$t$为根节点的子树$T_t$的损失函数是

$$C_{\alpha}(T_t) = C(T_t) + \alpha | T_t |$$

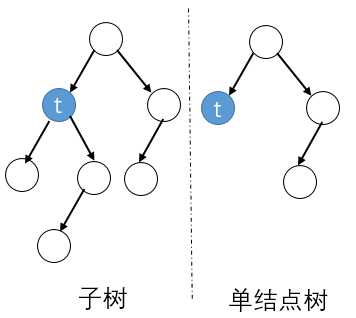
当$ \alpha=0 $及$\alpha$充分小时，有不等式

$$C_{\alpha}(T_t) < C_{\alpha}(t)$$

当$ \alpha $增大时，在某一$ \alpha $有

$$C_{\alpha}(T_t) = C_{\alpha} (t)$$

当$\alpha$增大时，不等式反向。只要$ \alpha=\frac{C(t)-C(T_t)}{| T_t | - 1} $，$T_t$与$t$具有相同的损失，但是$t$的结点数量更少，因此$t$更可取，所以剪枝。

对$T_0$中每一个内部结点$t$，计算

$$g(t) = \frac{C(t)-C(T_t)}{| T_t | - 1}$$

它表示间之后整体损失函数减少的程度，在$T_0$中减去$g(t)$最小的$T_t$，将得到的子树作为$T_1$，同时将最小的$g(t)$设为$\alpha$， $T_1$为区间[$\alpha_1,\alpha_2$]的最优子树。

这个地方理解为：最小的g(t)是一个阈值，选择$\alpha=\mathop{\min}\lbrace g(t) \rbrace \Longleftrightarrow$ [其他g(t)的情况是-剪枝比不剪枝的损失大，即式（16）不等号反向的情况]，所以在最小g(t)处剪枝

如此剪枝下去，直至得到根节点，在这个过程中，不断增加$\alpha$的值，产生新的区间。

• 1. 在剪枝得到的子树序列中通过交叉验证选取最优子树

利用独立的验证数据集，测试子树序列$ T_0,T_1,…,T_n $中各棵子树的平方误差或基尼指数，平方误差或基尼指数最小的决策树被认为是最优决策树，在子树序列中，每棵子树$ T_1,T_2,…,T_n $都对应着一个参数$ \alpha_1, \alpha_2, …, \alpha_n $，所以当最优子树$T_k$确定时，对应的$\alpha_k$也确定了，即得到最优决策树$T_\alpha$。

---

输入：CART算法生成的决策树$T_0$；

输出：最优决策树$T_\alpha$。

（1）设$k=0, \quad T=T_0$

（2）设$\alpha=0$

（3）自下而上地对各内部结点$t$计算$C(T_t)$，$| T_t | $以及

$$g(t)=\frac{C(t)-C(T_t)}{| T_t | - 1}$$ $$\alpha = \mathop{\min}(\alpha, g(t))$$

这里，$T_t$表示以$t$为根节点的子树，$C(T_t)$是对训练数据的预测误差，$ | T_t | $是$T_t$的叶结点个数。

（4）对$g(t)=\alpha$的内部结点$t$进行剪枝，并对叶结点$t$以多数表决法决定其类，得到树$T$。

（5）设$ k=k+1, \quad \alpha_k=\alpha, \quad T_k=T $。

（6）如果$T_k$不是由根结点及两个叶结点构成的树，则回到步骤（3）；否则令$T_k=T_n$。

（7）采用交叉验证法在子树序列$T_0,T_1,…,T_n$中选择最优子树$T_\alpha$。

---

5. 特点

• 优点：可解释性；可处理多种数值类型；没有复杂的参数设置；运算快
• 缺点：易过拟合；不适合高维数据；异常值敏感；泛化能力差

控制过拟合的方式

（1）树的深度
（2）一个结点被拆分出子结点所需要的包含最少的样本个数
（3）最底层结点所需要好汉的最小样本个数
（4）集成学习的方法(随机森林，Xgboost等)

连续值如何划分？

C45：基于阈值的信息增益(比)
CART：最优切分变量和最优切分点

缺失值如何处理？

概率权重(Probability Weights)：C45、ID3
替代法(Alternate/Surrogate Splits)：CART

不完整数据如何处理？ 决策树是如何处理不完整数据的？-知乎

（1）抛弃缺失值
抛弃极少量的缺失值的样本对决策树的创建影响不是太大。但是如果属性缺失值较多或是关键属性值缺失,创建的决策树将是不完全的,同时可能给用户造成知识上的大量错误信息,所以抛弃缺失值一般不采用。

（2）补充缺失值
缺失值较少时按照我们上面的补充规则是可行的。但如果数据库的数据较大,缺失值较多,这样根据填充后的数据库创建的决策树可能和根据正确值创建的决策树有很大变化。

（3）概率化缺失值
对缺失值的样本赋予该属性所有属性值的概率分布,即将缺失值按照其所在属性已知值的相对概率分布来创建决策树。用系数F进行合理的修正计算的信息量,“F=数据库中缺失值所在的属性值样本数量去掉缺失值样本数量/数据库中样本数量的总和”,即F表示所给属性具有已知值样本的概率。

---

6. 代码实现

代码中的公式均指李航老师的《统计学习方法》中的公式。

Decision_Tree.py

# coding:utf-8
import numpy as np
import pandas as pd

class DecisionTree(object):
    def __init__(self, feature_names, threshold, principle="information gain"):
        self.feature_names = feature_names
        self.threshold = threshold
        self.principle = principle
    # formula 5.7
    def __calculate_entropy__(self, y):
        datalen = len(y)
        labelprob = {l: 0 for l in set(y)}
        entropy = 0.0
        for l in y:
            labelprob[l] += 1
        for l in labelprob.keys():
            thisfrac = labelprob[l] / datalen
            entropy -= thisfrac * np.log2(thisfrac)
        return entropy
    # formula 5.8
    def __calculate_conditional_entropy__(self, X, y, axis):
        datalen = len(y)
        featureset = set([x[axis] for x in X])
        sub_y = {f:list() for f in featureset}
        for i in range(datalen):
            sub_y[X[i][axis]].append(y[i])
        conditional_entropy = 0.0
        for key in sub_y.keys():
            prob = len(sub_y[key]) / datalen
            entropy = self.__calculate_entropy__(sub_y[key])
            conditional_entropy += prob * entropy
        return conditional_entropy
    # formula 5.9
    def calculate_information_gain(self, X, y, axis):
        hd = self.__calculate_entropy__(y)
        hda = self.__calculate_conditional_entropy__(X, y, axis)
        gda = hd - hda
        return gda

    def __most_class__(self, y):
        labelset = set(y)
        labelcnt = {l:0 for l in labelset}
        for y_i in y:
            labelcnt[y_i] += 1
        st = sorted(labelcnt.items(), key=lambda x: x[1], reverse=True)
        return st[0][0]
    # formula 5.10
    def calculate_information_gain_ratio(self, X, y, axis):
        gda = self.calculate_information_gain(X, y, axis)
        had = self.__calculate_entropy__(X[:, axis])
        grda = gda / had
        return grda

    def __split_dataset__(self, X, y, axis, value):
        rstX = list()
        rsty = list()
        for i in range(len(X)):
            if X[i][axis] == value:
                tmpfeature = list(X[i][:axis])
                tmpfeature.extend(list(X[i][axis+1:]))
                rstX.append(tmpfeature)
                rsty.append(y[i])
        return np.asarray(rstX), np.asarray(rsty)

    def __best_split_feature__(self, X, y, feature_names):
        best_feature = -1
        max_principle = -1.0
        for feature_n in feature_names:
            axis = feature_names.index(feature_n)
            if self.principle == "information gain":
                this_principle = self.calculate_information_gain(X, y, axis)
            else:
                this_principle = self.calculate_information_gain_ratio(X, y, axis)
            print("%s\t%f\t%s" % (feature_n, this_principle, self.principle))
            if this_principle > max_principle:
                best_feature = axis
                max_principle = this_principle
        print("-----")
        return best_feature, max_principle

    def _fit(self, X, y, feature_names):
        # 所有实例属于同一类
        labelset = set(y)
        if len(labelset) == 1:
            return labelset.pop()
        # 如果特征集为空集，置T为单结点树，实例最多的类作为该结点的类，并返回T
        if len(feature_names) == 0:
            return self.__most_class__(y)
        # 计算准则,选择特征
        best_feature, max_principle = self.__best_split_feature__(X, y, feature_names)
        # 如果小于阈值，置T为单结点树，实例最多的类作为该结点的类，并返回T
        if max_principle < self.threshold:
            return self.__most_class__(y)

        best_feature_label = feature_names[best_feature]
        del feature_names[best_feature]
        tree = {best_feature_label: {}}

        bestfeature_values = set([x[best_feature] for x in X])
        for value in bestfeature_values:
            sub_X, sub_y = self.__split_dataset__(X, y, best_feature, value)
            tree[best_feature_label][value] = self._fit(sub_X, sub_y, feature_names)
        return tree

    def fit(self, X, y):
        feature_names = self.feature_names[:]
        self.tree = self._fit(X, y, feature_names)

    def _predict(self, tree, feature_names, x):
        firstStr = list(tree.keys())[0]
        secondDict = tree[firstStr]
        featIndex = feature_names.index(firstStr)
        key = x[featIndex]
        valueOfFeat = secondDict[key]
        if isinstance(valueOfFeat, dict):
            classLabel = self._predict(valueOfFeat, feature_names, x)
        else:
            classLabel = valueOfFeat
        return classLabel

    def predict(self, X):
        preds = list()
        for x in X:
            preds.append(self._predict(self.tree, self.feature_names, x))
        return preds

    def output_tree(self):
        import treePlot     # cite: https://gitee.com/orayang_admin/ID3_decisiontree/tree/master
        import importlib
        importlib.reload(treePlot)
        treePlot.createPlot(self.tree)

def load_data():
    dt = pd.read_csv("./credit.csv")    # from lihang - "statistic learning method" - page59, table 5.1
    # dt = pd.read_csv("./titanic.csv")
    data = dt.values
    feature_names = dt.columns[:-1] # delete label column
    return data, list(feature_names)

def run_ID3():
    data, feature_names = load_data()
    print("ID3 Descision Tree ... ")
    ml = DecisionTree(feature_names=feature_names, threshold=0, principle="information gain")
    ml.fit(data[:, :-1], data[:, -1])
    test = [["mid", "yes", "no", "good"]]
    preds = ml.predict(test)
    print("ID3 predict:", preds)
    ml.output_tree()

def run_C45():
    data, feature_names = load_data()
    print("C45 Descision Tree ... ")
    ml = DecisionTree(feature_names=feature_names, threshold=0, principle="information gain ratio")
    ml.fit(data[:, :-1], data[:, -1])
    test = [["mid", "yes", "no", "good"]]
    preds = ml.predict(test)
    print("C45 predict:", preds)
    ml.output_tree()

if __name__ == '__main__':
    # run_ID3()
    run_C45()

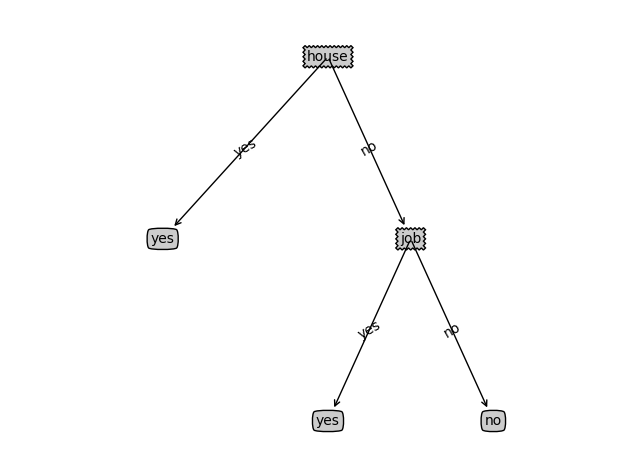
结果：

ID3 Descision Tree ... 
age    0.083007    information gain
job    0.323650    information gain
house    0.419973    information gain
credit    0.362990    information gain
-----
age    0.251629    information gain
job    0.918296    information gain
credit    0.473851    information gain
-----
ID3 predict: ['yes']

---

C45 Descision Tree ... 
age    0.052372    information gain ratio
job    0.352447    information gain ratio
house    0.432538    information gain ratio
credit    0.231854    information gain ratio
-----
age    0.164411    information gain ratio
job    1.000000    information gain ratio
credit    0.340374    information gain ratio
-----
C45 predict: ['yes']

---

7. 参考

李航 - 《统计学习方法》

zergzzlun - cart树怎么进行剪枝？

巩固,张虹 - 决策树算法中属性缺失值的研究

周志华 - 《机器学习》

OraYang的博客