逻辑斯谛回归 Logistic Regression

逻辑斯谛回归 - Logistic Regression

1. 逻辑斯谛分布

设 $ X $ 是连续随机变量，$ X $ 服从逻辑斯谛分布是指 $ X $ 具有下列分布函数和密度函数：

$F(x)=P(X\le{x})=\frac{1}{1+e^{-(x-\mu)/\gamma}}$ $f(x)=F'(x)=\frac{e^{-(x-\mu)/\gamma}}{\gamma(1+e^{-(x-\mu)/\gamma})^{2}}$

密度函数与分布函数图像如下,其中分布函数以$ (\mu,\frac{1}{2}) $中心对称。

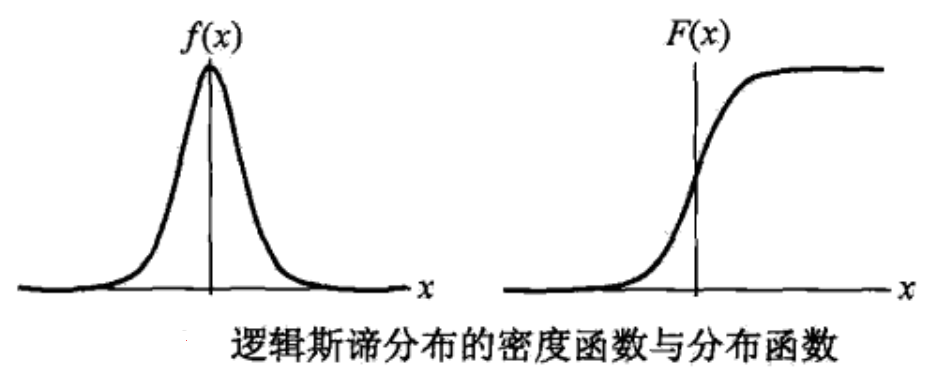
fenbu

2. 逻辑斯谛回归模型

$P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}$ $P(Y=0|x)=\frac{1}{1+exp(w\cdot x)}$

3. 逻辑斯谛模型的参数估计

设

$P(Y=1|x)=\frac{exp(w\cdot x)}{1+exp(w\cdot x)}=\pi(x)$ $P(Y=0|x)=\frac{1}{1+exp(w\cdot x)}=1-\pi(x)$

似然函数(N为样本数量)：

$l(w)=\prod_{i=1}^{N}[\pi(x_i)]^{y_i}[1-\pi(x_i)]^{1-y_i}$

对数似然：

$L(w)=logl(w)=\sum_{i=1}^N[y_ilog\pi(x_i)+(1-y_i)log(1-\pi(x_i))]$

对$ L(w) $求极值

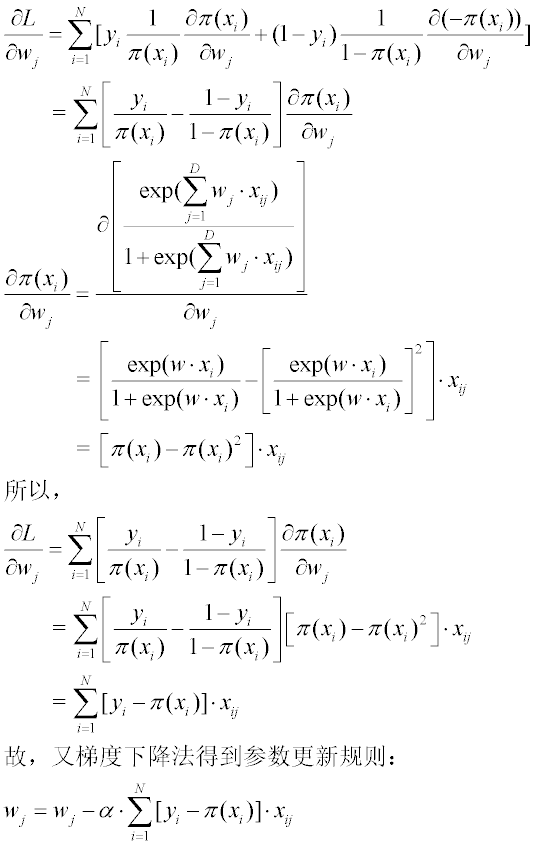
其中$ x_i $表示第$ i $个训练样例；$x_{ij} $表示第$ i $个训练样例的第$ j $个维度。

$ N $表示样本数量； $ D $表示样本维度。

4. 逻辑斯谛模型的特点

优点：

形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。

模型效果不错。在工程上是可以接受的（作为baseline)，如果特征工程做的好，效果不会太差，并且特征工程可以大家并行开发，大大加快开发的速度。

训练速度较快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化sgd发展比较成熟，训练的速度可以通过堆机器进一步提高，这样我们可以在短时间内迭代好几个版本的模型。

资源占用小，尤其是内存。因为只需要存储各个维度的特征值。

方便输出结果调整。逻辑回归可以很方便的得到最后的分类结果，因为输出的是每个样本的概率分数，我们可以很容易的对这些概率分数进行cutoff，也就是划分阈值(大于某个阈值的是一类，小于某个阈值的是一类)。

缺点：

准确率并不是很高。因为形式非常的简单(非常类似线性模型)，很难去拟合数据的真实分布。

很难处理数据不平衡的问题。举个例子：如果我们对于一个正负样本非常不平衡的问题比如正负样本比 10000:1.我们把所有样本都预测为正也能使损失函数的值比较小。但是作为一个分类器，它对正负样本的区分能力不会很好。

处理非线性数据较麻烦。逻辑回归在不引入其他方法的情况下，只能处理线性可分的数据，或者进一步说，处理二分类的问题。

逻辑回归本身无法筛选特征。有时候，我们会用gbdt来筛选特征，然后再上逻辑回归。

5. 代码实现

使用sklearn中的load_breast_cancer()作为二分类数据集。

Binary Logistic Regression 代码

# coding:utf-8
import time
import numpy as np
from datetime import timedelta
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_breast_cancer

def time_consume(s_t):
    diff = time.time()-s_t
    return timedelta(seconds=int(diff))

class BinaryLR(object):
    def __init__(self):
        self.weight = None
        self.learning_rate = 0.001
        self.max_iteration = 3000

    def predict_single_sample(self, feature):
        feature = list(feature)
        feature.append(1.0)
        wx = np.sum(np.matmul(self.weight, feature))
        exp_wx = np.exp(wx)
        if exp_wx/(1+exp_wx) > 0.5:
            return 1
        else:
            return 0

    def fit(self, X, y):
        self.nlen = X.shape[0]
        self.ndim = X.shape[1]
        self.weight = np.zeros(shape=self.ndim+1) # add bias to weight

        correct = 0
        exec_times = 0
        while exec_times < self.max_iteration:
            index = np.random.randint(0, self.nlen)
            feature = list(X[index])
            label = self.predict_single_sample(feature)

            if label == y[index]:
                correct += 1
                if correct > self.max_iteration:
                    break
                continue

            exec_times += 1
            correct = 0

            feature.append(1.0)
            wx = np.sum(np.matmul(self.weight, feature))
            exp_wx = np.exp(wx)

            # update weight
            for i in range(self.weight.shape[0]):
                self.weight[i] -= self.learning_rate * (label - exp_wx / (1.0 + exp_wx)) * feature[i]

            if exec_times % 100 == 0:
                print("Times:%d TrainAcc:%.4f Timeusage:%s" % (exec_times, self.accuracy(train_y, self.predict(train_x)), time_consume(start_time)))

    def predict(self, X):
        if self.weight is None:
            raise ValueError("Please train model first.")

        labels = list()
        for i in range(X.shape[0]):
            d = X[i]
            labels.append(self.predict_single_sample(d))
        return labels

    def accuracy(self, y_true, y_pred):
        return accuracy_score(y_true, y_pred)

def load_dataset():
    data = load_breast_cancer()
    return data.data, data.target


if __name__ == '__main__':
    start_time = time.time()

    data, target = load_dataset()
    print("Data Shape:", data.shape, target.shape)

    train_x, test_x, train_y, test_y = train_test_split(data, target, test_size=0.3, random_state=1024, shuffle=True)

    ml = BinaryLR()
    ml.fit(train_x, train_y)
    y_pred = ml.predict(test_x)
    accuracy = ml.accuracy(test_y, y_pred)
    print("Accuracy is ", accuracy)
    print("Timeusage: %.2f s" % (time.time()-start_time))

运行结果如下：（不同的划分会产生不同的结果，且差异比较大）

Times:100 TrainAcc:0.8518 Timeusage:0:00:00
Times:200 TrainAcc:0.8518 Timeusage:0:00:00
Times:300 TrainAcc:0.8518 Timeusage:0:00:00
Times:400 TrainAcc:0.8518 Timeusage:0:00:00
Times:500 TrainAcc:0.8518 Timeusage:0:00:00
Times:600 TrainAcc:0.8518 Timeusage:0:00:00
Times:700 TrainAcc:0.8518 Timeusage:0:00:00
Times:800 TrainAcc:0.8518 Timeusage:0:00:00
Times:900 TrainAcc:0.8518 Timeusage:0:00:00
Times:1000 TrainAcc:0.8518 Timeusage:0:00:00
Times:1100 TrainAcc:0.8518 Timeusage:0:00:00
Times:1200 TrainAcc:0.8518 Timeusage:0:00:00
Times:1300 TrainAcc:0.8518 Timeusage:0:00:00
Times:1400 TrainAcc:0.8518 Timeusage:0:00:00
Times:1500 TrainAcc:0.8518 Timeusage:0:00:00
Times:1600 TrainAcc:0.8518 Timeusage:0:00:00
Times:1700 TrainAcc:0.8518 Timeusage:0:00:00
Times:1800 TrainAcc:0.8518 Timeusage:0:00:00
Times:1900 TrainAcc:0.8518 Timeusage:0:00:00
Times:2000 TrainAcc:0.8518 Timeusage:0:00:00
Times:2100 TrainAcc:0.8518 Timeusage:0:00:00
Times:2200 TrainAcc:0.8518 Timeusage:0:00:00
Times:2300 TrainAcc:0.8518 Timeusage:0:00:00
Times:2400 TrainAcc:0.8518 Timeusage:0:00:00
Times:2500 TrainAcc:0.8518 Timeusage:0:00:00
Times:2600 TrainAcc:0.8518 Timeusage:0:00:00
Times:2700 TrainAcc:0.8518 Timeusage:0:00:00
Times:2800 TrainAcc:0.8518 Timeusage:0:00:00
Times:2900 TrainAcc:0.8518 Timeusage:0:00:00
Times:3000 TrainAcc:0.8518 Timeusage:0:00:00
Accuracy is  0.877192982456
Timeusage: 0.71 s

面试常问

逻辑回归的损失函数为什么要使用极大似然函数作为损失函数？

损失函数一般有四种，平方损失函数，对数损失函数，HingeLoss0-1损失函数，绝对值损失函数。将极大似然函数取对数以后等同于对数损失函数。在逻辑回归这个模型下，对数损失函数的训练求解参数的速度是比较快的。

$\theta_j = \theta_j - (y_i - h_{\theta}(x_i)) \cdot x_{ij}$

更新速度只和$ x_{ij}，y_i $相关。和sigmod函数本身的梯度是无关的。这样更新的速度是可以自始至终都比较的稳定。

为什么不选平方损失函数的呢？其一是因为如果你使用平方损失函数，你会发现梯度更新的速度和 sigmod 函数本身的梯度是很相关的。 sigmod函数在它在定义域内的梯度都不大于0.25。这样训练会非常的慢。

逻辑回归在训练的过程当中，如果有很多的特征高度相关或者说有一个特征重复了100遍，会造成怎样的影响？

先说结论，如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。

但是对特征本身来说的话，假设只有一个特征，在不考虑采样的情况下，你现在将它重复100遍。训练以后完以后，数据还是这么多，但是这个特征本身重复了100遍，实质上将原来的特征分成了100份，每一个特征都是原来特征权重值的百分之一。

如果在随机采样的情况下，其实训练收敛完以后，还是可以认为这100个特征和原来那一个特征扮演的效果一样，只是可能中间很多特征的值正负相消了。

为什么我们还是会在训练的过程当中将高度相关的特征去掉？

去掉高度相关的特征会让模型的可解释性更好

可以大大提高训练的速度。如果模型当中有很多特征高度相关的话，就算损失函数本身收敛了，但实际上参数是没有收敛的，这样会拉低训练的速度。其次是特征多了，本身就会增大训练的时间。

参考：

李航 - 《统计学习方法》

周志华 - 《机器学习》

scikit-learn

WenDesi’s Github