二分查找 - BinarySearch

发表于 更新于 分类于

详细原文这里：特别好用的二分查找法模板

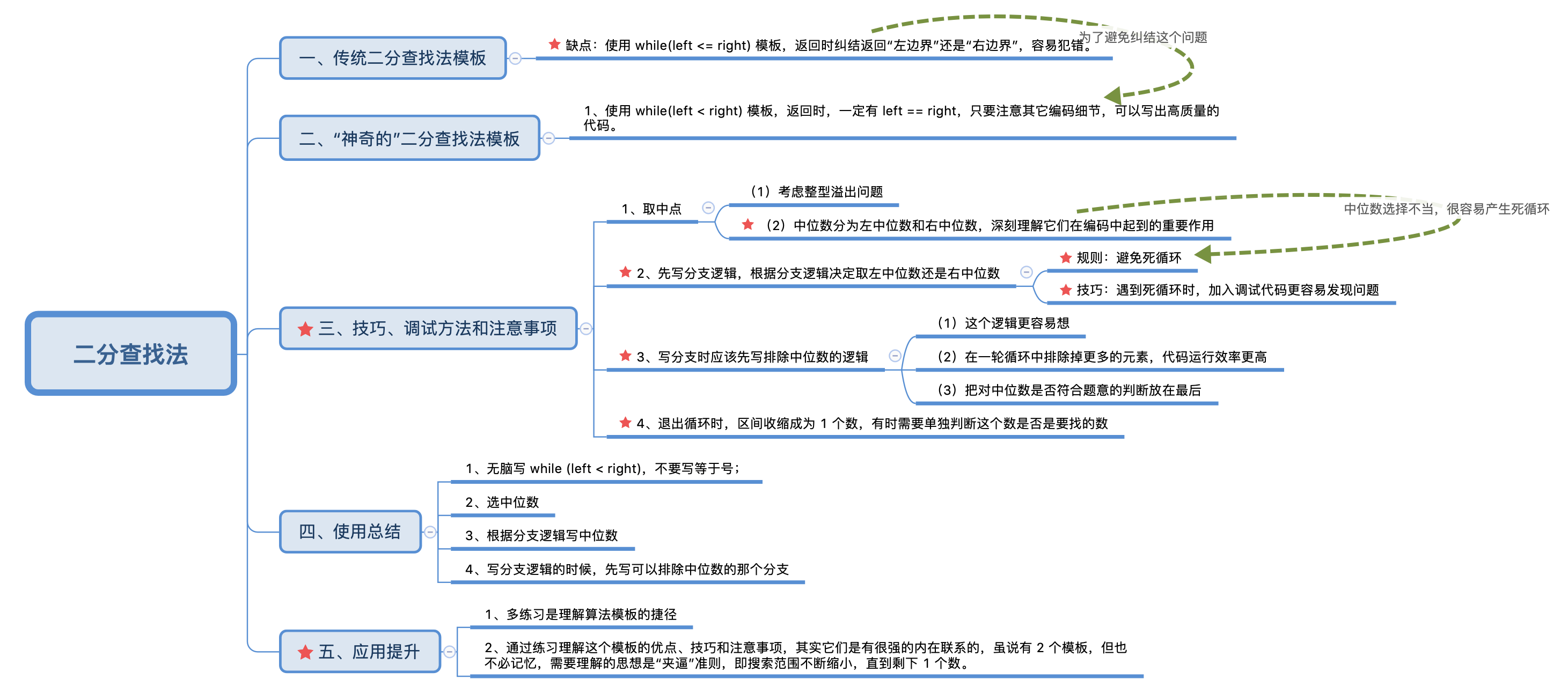
1. 二分查找的基本思想

二分查找的基本思想是：夹逼法或者叫排除法

在每一轮循环中，都可以排除候选区间里将近一半的元素，进而使得候选区间越来越小，直至有限个数（通常为1个），而这个数就有可能是我们要找的数（在一些情况下，还需要单独做判断）。

2. 编码的细节

  1. 思考左右边界，如果左右边界不能包括目标数值，二分查找法是怎么都写不对的；
  2. 先写逻辑上容易想到的分支逻辑，这个分支逻辑通常是排除中位数的逻辑；
  3. 只写两个分支，一个分支排除中位数，另一个分支不排除中位数；
  4. 根据分支的逻辑选择中位数的类型，可能是左中位数，也可能是右中位数，标准是避免出现死循环；
  5. 退出循环的时候，可能需要对夹逼法剩下的那个数做一次判断，这一步叫做后处理

3. 细节思考

  1. 参考代码 1：重点理解为什么候选区间的索引范围是 [0, size]。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
from typing import List

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        # 返回大于等于 target 的索引，有可能是最后一个
        size = len(nums)
        # 特判
        if size == 0:
            return 0

        left = 0
        # 如果target比nums里所有的数都大，则最后一个数的索引+1就是候选值，因此右边界应该是数组的长度
        right = size
        # 二分的逻辑一定要写对，否则会出现死循环或者数组下标越界
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] < target:
                left = mid + 1
            else:
                assert nums[mid] >= target
                # [1,5,7] 2
                right = mid
        return left
  1. 参考代码 2：对于是否接在原有序数组后面单独判断，不满足的时候再在候选区间的索引范围 [0, size-1] 内使用二分查找法进行搜索。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from typing import List

class Solution:

    def searchInsert(self, nums: List[int], target: int) -> int:
        # 返回大于等于 target 的索引，有可能是最后一个
        size = len(nums)
        # 特判 1
        if size == 0:
            return 0
        # 特判 2：如果比最后一个数字还要大，直接接在它后面就可以了
        if target > nums[-1]:
            return size

        left = 0
        right = size - 1
        # 二分的逻辑一定要写对，否则会出现死循环或者数组下标越界
        while left < right:
            mid = left + (right - left) // 2
            if nums[mid] < target:
                left = mid + 1
            else:
                assert nums[mid] >= target
                right = mid
        return left

4. 技巧&调试方法&注意事项

  1. 先来看int mid = left + (right - left) / 2， 其中left和right都是可以取到的数组index

    • 当 left 和 right 是很大的整数的时候，如果写int mid = (left + right) / 2; 这里 left + right 的值就有可能超过 int 类型能表示的最大值， 因此使用 mid = left + (right - left) // 2 可以避免这种情况。
    • 事实上，mid = left + (right - left) // 2 在 right 很大、 left 是负数且很小的时候， right - left 也有可能超过 int 类型能表示的最大值， 只不过一般情况下 left 和 right 表示的是数组索引值，left 是非负数，因此 right - left 溢出的可能性很小。
    • 建议在Java中用 (left + right) >>> 1，在Python中用 (left + right) >> 1，都是无符号右移。

  2. 当数组的元素个数是偶数的时候，中位数有左中位数和右中位数之分：

    • 当数组的元素个数是偶数的时候：
      • 使用 mid = left + (right - left) // 2 得到左中位数的索引；
      • 使用 mid = left + (right - left + 1) // 2 得到右中位数的索引。
    • 当数组的元素个数是奇数的时候，以上二者都能选到最中间的那个中位数。

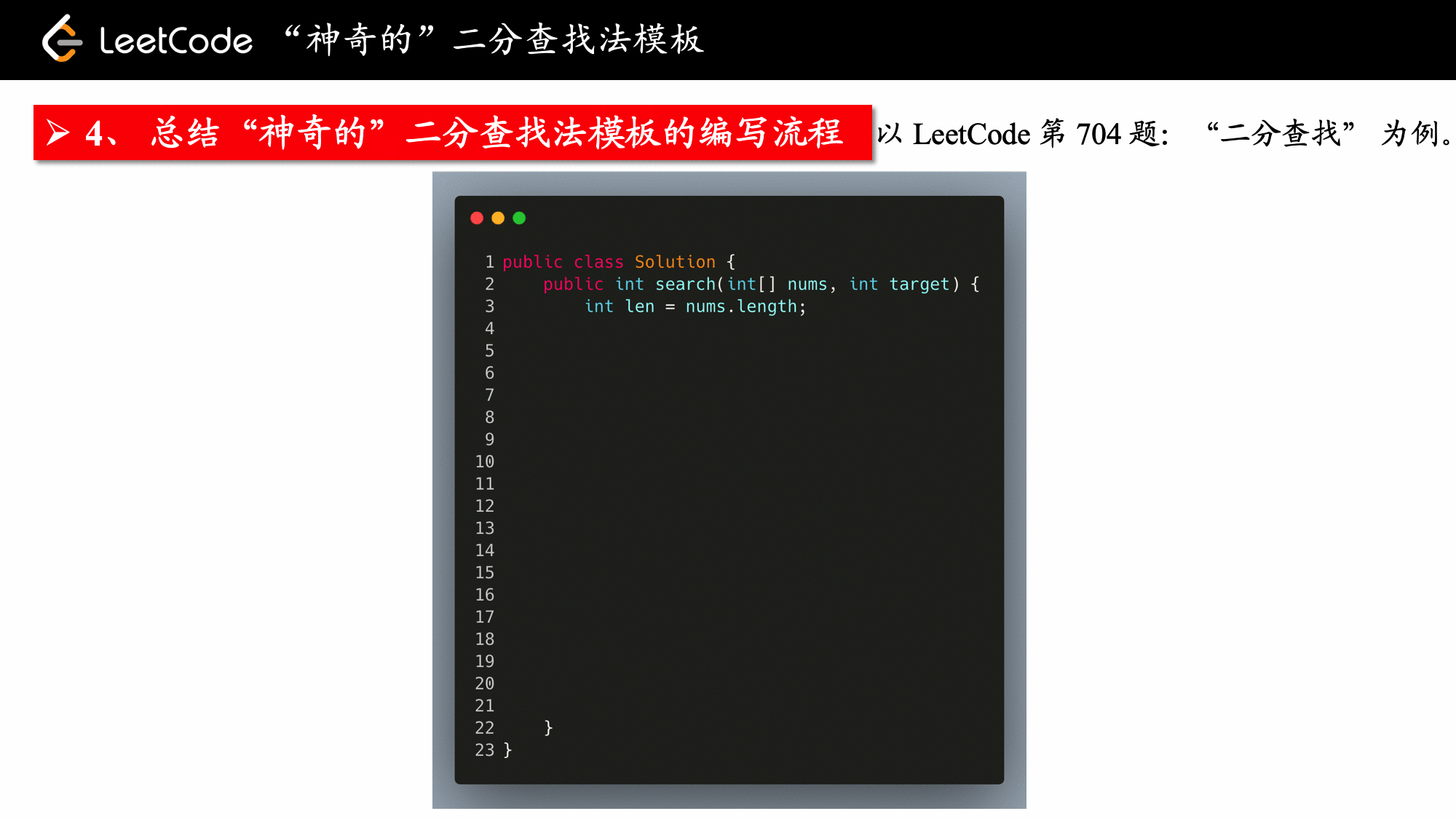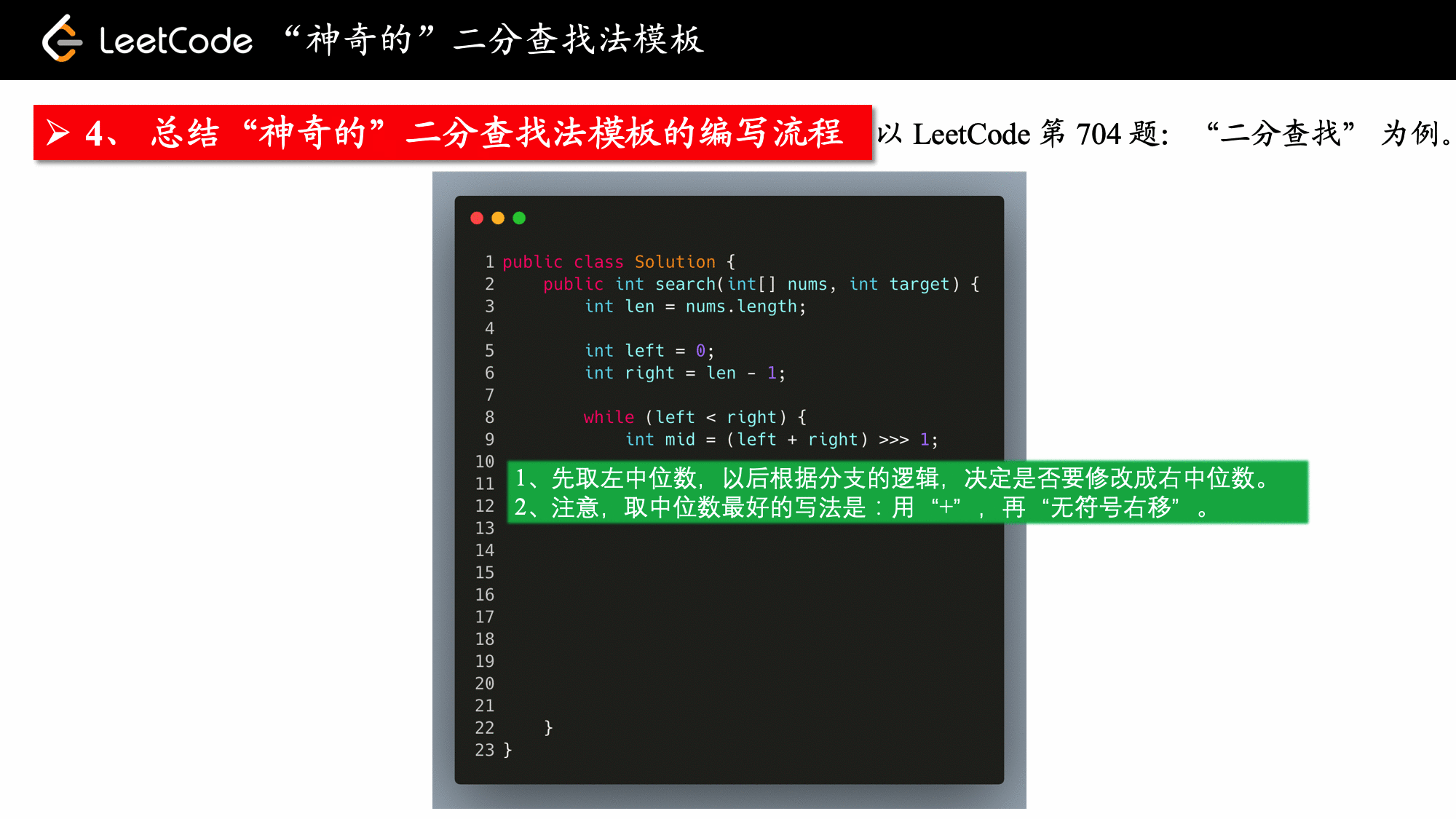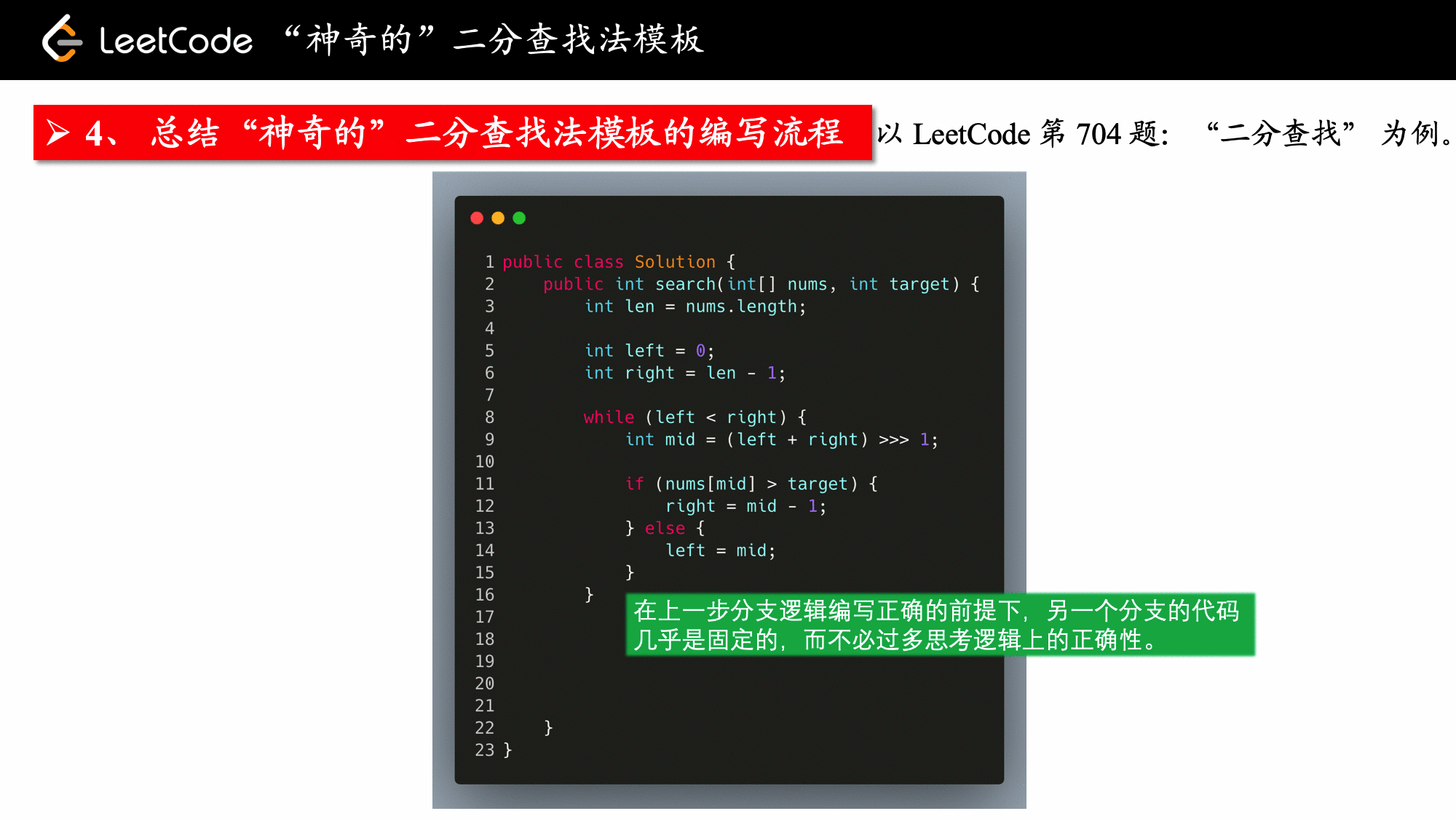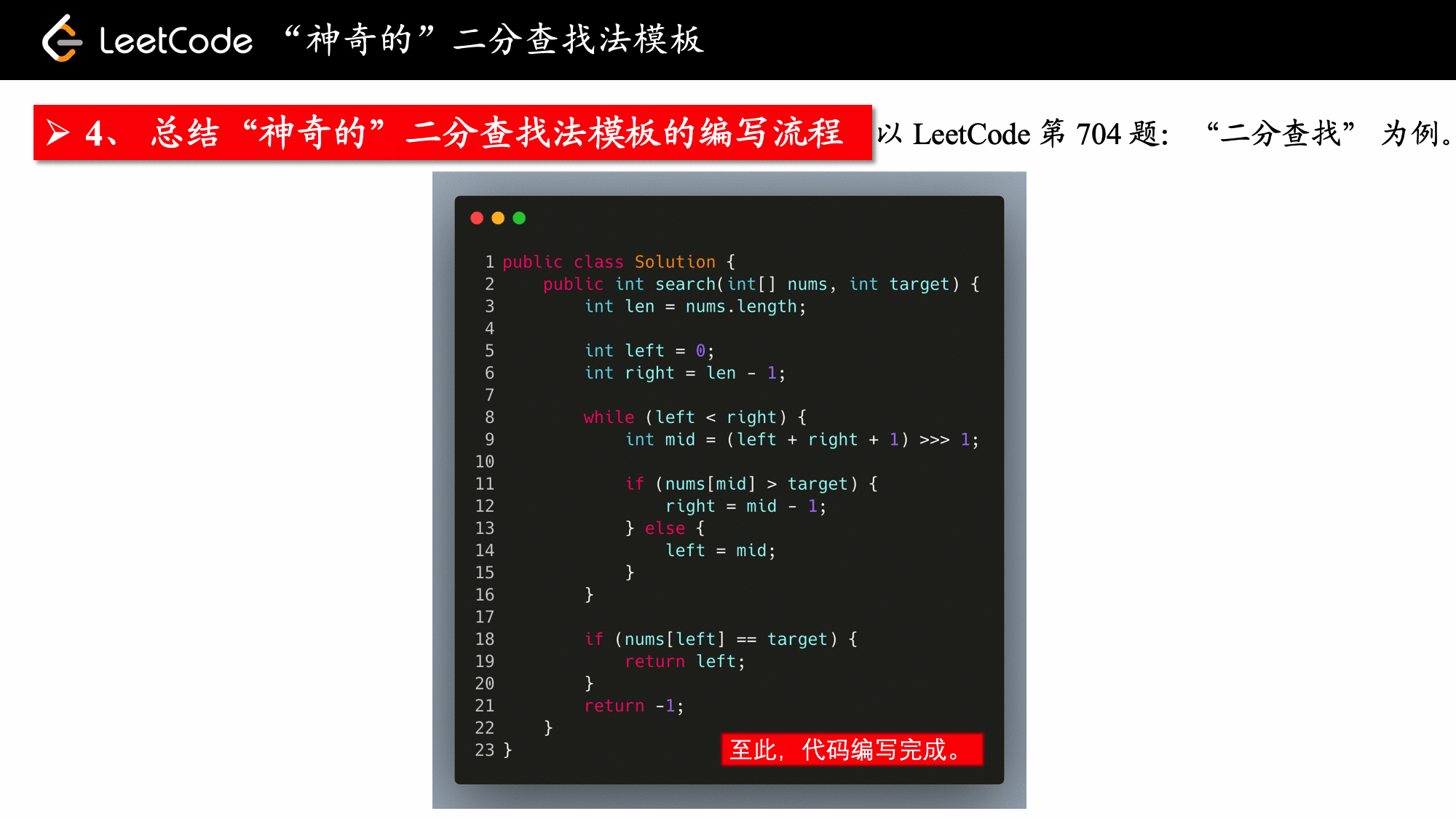
  3. 编写分支逻辑的时候，先写 “排除逻辑” 所在的分支。

    • 先考虑能把 “中位数” 排除在外的逻辑，而不能排除 “中位数” 的逻辑放在 else 分支里，这样做的理由有 2点：
      • 可以排除 “中位数” 的逻辑，通常比较好想，但并不绝对，这一点视情况而定
      • 分支条数变成 2 条，比原来 3 个分支要考虑的情况少，好处是: 不用在每次循环开始单独考虑中位数是否是目标元素，节约了时间，我们只要在退出循环的时候，即左右区间压缩成一个数（索引）的时候，去判断这个索引表示的数是否是目标元素，而不必在二分的逻辑中单独做判断。

  4. 根据分支编写的情况，选择使用左中位数还是右中位数

    • 先写判断分支，根据分支的逻辑选中位数，选左中位数还是右中位数，这要做的理由是为了防止出现死循环。死循环容易发生在区间只有 2 个元素时候，此时中位数的选择尤为关键。
    • 当出现死循环的时候的调试方法：打印输出左右边界、中位数的值和目标值、分支逻辑等必要的信息

5. 使用总结

  1. 无脑地写 while left < right: ，这样你就不用判断，在退出循环的时候你应该返回 left 还是 right，因为返回 left 或者 right 都对；
  2. 先写分支逻辑，并且先写排除中位数的逻辑分支（因为更多时候排除中位数的逻辑容易想），另一个分支的逻辑你就不用想了，写出第1个分支的反面代码即可，再根据分支的情况选择使用左中位数还是右中位数；左右分支的规律就如下两点：
    • 如果第 1 个分支的逻辑是 “左边界排除中位数”（left = mid + 1），那么第 2 个分支的逻辑就一定是 “右边界不排除中位数”（right = mid），反过来也成立；这种情况的时候选择左中位数，即加一选左。
    • 如果第 2 个分支的逻辑是 “右边界排除中位数”（right = mid - 1），那么第 2 个分支的逻辑就一定是 “左边界不排除中位数”（left = mid），反之也成立；这种情况的时候选择右中位数，即减一选右。
  3. 分支条数只有 2 条，代码执行效率更高，不用在每一轮循环中单独判断中位数是否符合题目要求，写分支的逻辑的目的是尽量排除更多的候选元素，而判断中位数是否符合题目要求我们放在最后进行；
  4. 注意事项
    • 左中位数还是右中位数选择的标准根据分支的逻辑而来，标准是每一次循环都应该让区间收缩，当候选区间只剩下 2 个元素的时候，为了避免死循环发生，选择正确的中位数类型。 如果实在很晕，不防使用有 2 个元素的测试用例，另外在代码出现死循环的时候，建议可以将左边界、右边界、你选择的中位数的值，还有分支逻辑都打印输出一下，出现死循环的原因就一目了然了；
    • 如果能确定要找的数就在候选区间里，那么退出循环的时候，区间最后收缩成为 1 个数后，直接把这个数返回即可； 如果你要找的数有可能不在候选区间里，区间最后收缩成为 1 个数后，还要单独判断一下这个数是否符合题意。

6. 模版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Python: 当分支逻辑不能排除右边界时，选左中位数；如果选右中位数会出现死循环
def binary_search_template1(left, right):
    # 如果选择右中位数，当区间只剩下2个元素时，
    # 一旦进入 right=mid 这个分支，右边界不会收缩，会进入死循环
    while left < right:
        # 选择左中位数，无符号右移
        mid = (left + right) >> 1
        if check(mid):
            # 先写排除中位数的逻辑
            left = mid + 1
        else:
            # 右边界不能排除
            right = mid

    # 退出循环时一定有 left == right
    # 视情况分析是否需要单独判断 left(或者right) 这个索引表示的元素是否符合题意
    pass
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# Python: 当分支逻辑不能排除左边界时，选右中位数；如果选左中位数会出现死循环
def binary_search_template2(left, right):
    # 如果选择左中位数，当区间只剩下2个元素时，
    # 一旦进入 left=mid 这个分支，右边界不会收缩，会进入死循环
    while left < right:
        # 选右中位数
        mid = (left + right + 1) >> 1
        if check(mid):
            # 先写排除中位数的逻辑
            right = mid - 1
        else:
            # 左边界不能排除
            left = mid
    # 退出循环时一定有 left == right
    # 视情况分析是否需要单独判断 left(或者right) 这个索引表示的元素是否符合题意
    pass

虽说是两个模板，区别在于选中位数，中位数根据分支逻辑来选，原则是区间要收缩，且不出现死循环，退出循环的时候，视情况，有可能需要对最后剩下的数单独做判断。

7. 二分排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 时间复杂度：O(n) * O(logn) = O(nlogn)
void binarysort(vector<int> &arr) {
    int start, end, tmp = 0, mid, j;
    // 每次将 arr[i] 插入到排好序的 arr[0:i-1] 中，时间复杂度 O(n)
    for (int i = 1; i < arr.size(); i++) {
        start = 0; 
        // arr[i] 可能就是较大的，要放在arr[i]的位置，因此 end = i
        end = i; 
        // 待插入的值tmp
        tmp = arr[i];
        // 二分查找到要插入的index，时间复杂度 O(logn)
        while (start < end) {
            mid = (start + end) >> 1;
            if (arr[mid] < tmp)
                start = mid + 1;
            else
                end = mid;
        }
        // 往后挪值
        for (j = i - 1; j >= start; j--) {
            arr[j + 1] = arr[j];
        }
        // 插入
        arr[start] = tmp;
    }
}
0%